Closed Subsets and Bases for a Topology
[math Published June 17, 2020
Subconjuntos cerrados
Definición (Subconjunto cerrado) : Dado un espacio topológico \((X,\tau)\), se dice que un subconjunto \(U\subseteq X\) es cerrado si su complemento es un conjunto abierto.
De aquí en adelante usaremos siempre que \((X,\tau)\) es un espacio topológico.
Otra forma de verlo es: \(U\) es cerrado si \(U/X\in\tau\).
Ahora, introduciremos el concepto de clausura de un subconjunto:
Definición (Clausura) : Sea \(A\subseteq X\), definimos a la clausura de \(A\) como la intersección de todos los cerrados de \(X\) que contienen a \(A\): \(\bar A = \bigcap\{F\subseteq X: F \text{ es cerrado y } A\subseteq F \} \tag{1}\)
A los puntos que pertenecen a la clausura de un conjunto se les llaman punto límite .
Ahora veremos algunas propiedades de la clausura de un conjunto:
-
\(\bar A\) es cerrado: Se puede ver a partir de la ecuación (1). La intersección de conjuntos cerrados es un conjunto cerrado.
-
Si \(A\subseteq B\implies \bar A\subseteq \bar B\)
-
Si \(A\) es cerrado \(\implies A=\bar A\): Esta propiedad refiere al hecho de que un conjunto cerrado contiene a todos sus puntos límites.
-
\(\bar (\bar A) = \bar A\).
-
\(\bar A\) es el menor cerrado que contiene a \(A\).
-
\bar{A\cup B} = \bar A\cup\bar B.
Bases for a Topology
A veces resulta una tarea muy tediosa o dificil escribir toda la topología para un conjunto. Es por eso que a veces resulta más fácil dar una base que genere la topología. Por generar uno se refiere a que todo elemento de la topología es la unión finita de algunos (o todos) elementos de la base.
Comenzamos definiendo una base:
Definición (Base para una topología): Una familia de conjuntos \(\mathscr{B}\) que satisfacen las siguientes propiedades:
- Para cada elemento \(x\in X\) existe siempre un elemento de la base \(B\in\mathscr{B}\) tal que \(x\in B\).
- Si \(x\) pertenece a la intersección de dos elementos de la base \(B_1\cap B_2\) siempre existe otro elemento \(B_3\subset B_1\cap B_2\) que contiene a \(x\).
Ahora debemos explicar como es que esta base genera una topología \(\tau\).
Decimos que un subconjunto \(U\subset X\) es abierto (es decir que \(U\) es un elemento de la topología) si existe \(B\in\mathscr{B}\) tal que para todo \(x\in U\implies x\in B\) y \(B\subset U\).
De esto podemos razonar fácilmente que todo elemento de la base \(\mathscr{B}\) es un elemento de la topología \(\tau\).
Ahora veamos algunos ejemplos de bases.
Ejemplo 1 . Sea \(\mathscr{B}\) la familia de regiones circulares en el plano. Se puede comprobar que cumple ambas condiciones de base. En la imagen se muestra la comprobación de la segunda propiedad.
Ejemplo 2 . Sea \(\mathscr{B}'\) la familia de rectángulos con los lados paralelos a los ejes del plano. Se puede ver que también cumple con las propiedades de una base. En este caso, la segunda condición se cumple ya que la intersección de dos rectángulos es vacía u otro rectángulo.
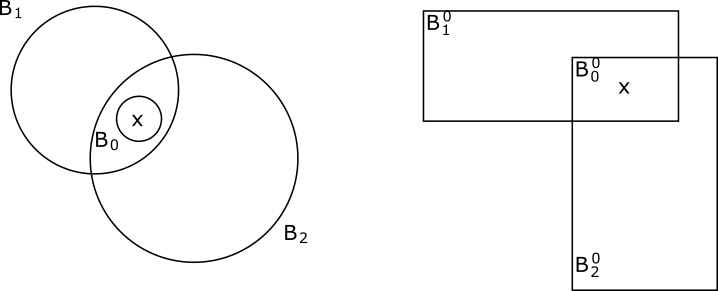
Hasta ahora no verificamos que efectivamente \(\tau\) es una topología.
Recordemos que para que una familia de conjuntos sea una topología se debían de cumplir 3 condiciones:
- El elemento vacío \(\empty\) y \(X\) pertenecen a la topología.
- La unión de elementos de la topología está en la topología.
- La intersección finita de elementos también está dentro de la topología.
Entonces, comprobemos estas tres condiciones. Tomemos una familia de elementos de \(\tau\) indexada como \(\{U_{\alpha} \}_\alpha\) y mostremos que \(U=\bigcup_\alpha U_\alpha\) pertenece a \(\tau\).
Agarremos \(x\in U\), entonces por lógica debe existir algún índice \(\alpha\) tal que \(x\in U_\alpha\). Ya que todos los \(U_\alpha\) son abierto ya que pertenecen en la topología existe un elemento de la base \(B\in\mathscr{B}\) tal que \(x\in B\subset U_\alpha\). Entonces, acabamos de mostrar que \(x\in B\) y \(B\subset U_\alpha \subset U\) , entonces por definición \(U\) es un abierto. Por lo tanto la unión de elementos de \(\tau\) está en \(\tau\).
Ahora sean \(U_1,U_2\in \tau\). Ahora elijamos dos elementos de la base , \(B_1\subset U_1\) y \(B_2\subset U_2\). Listo, ahora dado un elemento en la intersección \(x\in U_1\cap U_2\) y por la segunda propiedad de una base existe un tercer elemento \(B_3\subset B_1\cap B_2\) tal que \(x\in B_3\) . Entonces \(x\in B_3\) y \(B_3\subset U_1\cap U_2\) entonces la intersección es un conjunto abierto por definición. Sin embargo, no hemos terminado con la demostración: debemos probar que esto es verdad para la intersección finita de elementos de la topología. Para esto usamos algo que se aprende en todo curso de Algebra en la Universidad o incluso en la secundaria = inducción :) .
\(U_1\cap U_2\cap \cdots\cap U_n \tag{2}\)
El caso \(n=1\) es trivial ya que cada uno de los \(U_\alpha\) pertenece a \(\tau\).
Ahora suponemos que \(U_1\cap U_2\cap \dots \cap U_{n-1}\in \tau\) y probamos para el caso general \(n\):
\(U_1\cap U_2\cap \cdots\cap U_n = (U_1\cap U_2\cap \dots \cap U_{n-1}) \cap U_n \tag{3}\)
Pero antes mostramos que la intersección de dos elementos de la topología es un elemento de la topología, entonces \(U_1\cap U_2\cap \dots \cap U_{n}\in \tau\).
\(\therefore\) \(\tau\) generado por \(\mathscr{B}\) es una topología. !!
En el próximo post hablaremos sobre algunos lemas importantes que relacionan los elementos de la base con la topologia que generan y tambien sobre como saber la base que genera cierta topologia, es decir, el proceso inverso a lo visto hoy.