Covariant solution of Maxwell Equations
[physics Published June 29, 2020
Covariant Maxwell Equations
Las ecuaciones de Maxwell se pueden escribir en forma covariante en función de los tensores electromagnéticos \(F^{\mu\nu}\) y \(\tilde{F}^{\mu\nu}\) como:
\(\begin{align}
\partial_\mu F^{\mu\nu} &= \mu_0 J^\nu \label{eq:1} \tag{1} \\
\partial_\mu \tilde{F}^{\mu\nu} &= 0 \tag{2}
\end{align}\)
Estas ecuaciones se resuelven proponiendo que el tensor de campos se deriva de un cuadripotencial de acuerdo a :
\(F^{\mu\nu} = \partial_\mu A_\nu-\partial_\nu A_\mu \tag{3}\)
Esto permite escribir a \(\eqref{eq:1}\) como :
\(\square A^\nu-\partial^\nu(\partial_\mu A^\mu) = \mu_0 J^nu \label{4} \tag{4}\)
Podemos elegir el gauge de Lorentz en donde \(\partial_\mu A_\mu =0\) . Entonces, lo que queda es una ecuación de onda no homogénea:
\(\square A^\nu = \frac 1 {c^2}\frac{\partial^2 A^\nu}{\partial t^2}-\nabla^2 A^\nu =\mu_0 J^\nu \label{eq:5} \tag{5}\)
Esta ecuación se resuelve hallando la función de Green del problema. Básicamente, la función de Green es una función que cumple:
\(\square G(x^\mu,x'^\mu) = 4\pi \delta^{(4)}(x^\mu-x'^\mu) \label{eq:6} \tag{6}\)
Una vez que se ha hallado la función de Green las soluciones se escriben como :
\(A^\nu(x^\mu) = \frac{\mu_0}{4\pi}\int d^4x' G(x^\mu,x'^\mu)J^\nu(x'^\mu) \label{eq:7} \tag{7}\)
Esto se verifica fácilmente aplicando \(\square\) a \(\eqref{eq:7}\) :
\(\begin{align}\label{eq:8}\tag{8}
\square A^\nu &= \frac{\mu_0}{4\pi}\int d^4x' \square G(x^\mu,x'^\mu) J^\nu(x'^\mu) \\
&= \frac{\mu_0}{4\pi}\int d^4x' 4\pi \delta^{(4)}(x^\mu-x'^\mu)J^\nu(x'^\mu) \\
&= \mu_0 J^\nu(x^\mu)
\end{align}\)
Ahora, el problema se centra en hallar la función de Green resolviendo \(\eqref{eq:6}\) . Primero, debemos notar que la función de Green tiene simetría translacional. Esto se puede ver si hacemos el cambio \(x^\mu\rightarrow x^\mu+\epsilon^\mu\) y \(x'^\mu\rightarrow x'^\mu+\epsilon^\mu\). Esto permite redefinir a \(G\) como una función de \(z^\mu=x^\mu-x'^\mu\) tal que se cumple que,
\(\square G(z^\mu) = 4\pi \delta^{(4)}(z^\mu) \label{eq:9} \tag{9}\)
Para resolver \(\eqref{eq:9}\) recurrimos a la transformada de Fourier definida por:
\(\hat{F}(k_\mu):=\int d^4x F(x^\mu)e^{-ik_\mu x^\mu} \label{eq:10} \tag{10}\)
Y por consiguiente la transformada inversa se define como :
\(F(x_\mu) := \frac 1 {(2\pi)^4}\int d^4k \hat{F}(k_\mu)e^{ik_\mu x^\mu} \label{eq:11} \tag{11}\)
Ahora, para poder reescribir \(\eqref{eq:9}\) con las transformadas de Fourier, hallamos la transformada de la función delta espacio temporal:
\(\hat{\delta}^{(4)}(k_\mu) = \int d^3x \delta^{(4)}(x^\mu)e^{-ik_\mu x^{\mu}} = 1 \label{eq:12} \tag{12}\)
Esto permite escribir a la delta como :
\(\delta^{(4)}(x^\mu) = \frac 1 {(2\pi)^4}\int d^4k e^{ik_\mu x^\mu} \label{eq:13} \tag{13}\)
Entonces, reescribimos \(\eqref{eq:9}\) como:
\(\square\frac{1}{(2\pi)^4}\int d^4k \hat{G}(k_\mu) e^{ik_\mu x^\mu} = \frac{4\pi}{(2\pi)^4}\int d^4k e^{ik_\mu x^\mu} \label{eq:14} \tag{14}\)
El operador \(\square\) puede entrar a la integral y actuar sobre la exponencial, esto es, \(\square (e^{ik_\mu x^\mu})=i^2k_\mu k^\mu=-k_\mu k^\mu\). Lo que queda es pasar la integral de la izquierda a la derecha e igualar el integrando a cero. Esto es,
\(\int d^4k \left(\hat{G}(k_\mu)(-k_\mu k^\mu)-4\pi \right)e^{ik_\mu x^\mu}=0 \label{eq:15} \tag{15}\)
Entonces la funcion de Green transformada es:
\(\hat{G}(k_\mu)=-\frac{4\pi}{k_\mu k^\mu} \label{eq:16} \tag{16}\)
Lo que nos resta hacer ahora es antitransformar , con lo que la función de Green requerida es:
\(G(z^\mu) = -\frac{4\pi}{(2\pi)^4}\int d^4k \frac{e^{ik_\mu x^\mu}}{k_\mu k^\mu} = -\frac{1}{4\pi^3}\int d^3k e^{-i\vec{k}\cdot\vec{z}}\int_{-\infty}^{\infty} dk_0 \frac{e^{ik_0z^0}}{k_0^2-|\vec{k}|^2} \label{eq:17} \tag{17}\)
Doing the integral
Ahora procedemos a calcular la integral de \(\eqref{eq:17}\) . La integral es resoluble por medio de integrales de contorno. Vemos que existen polos simples de la variable \(k_0\) en los puntos \(\pm k\). Para resolver la integral debemos elegir un camino de integración. Podemos usar el camino de la Figura 1 o Figura 2 dependiendo del signo de \(z^0\) .
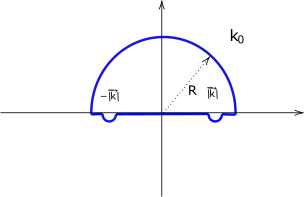

Llamemos a estas curvas \(\mathscr{C}_U\) y \(\mathscr{C}_L\) respectivamente . Pasemos la integral al plano complejo :
\[\oint_{\mathscr{C}} dk_0 \frac{e^{ik_0z^0}}{k_0^2-k^2} \label{eq:18} \tag{18}\]El factor \(e^{ik_0z^0}\) que acompaña al integrando es el que hace que la integración dependa del signo de \(z^0\) pues:
\[e^{ik_0z^0} = e^{iRe[k_0]z^0}e^{-Im[k_0]z^0} \label{eq:19} \tag{19}\]Si \(z^0>0\) conviene elegir \(\mathscr{C}_U\) ya que la parte imaginaria de \(k_0\) seria positiva y la expresión tendería a cero para \(R\rightarrow \infty\) . Escribamos \(\eqref{eq:18}\) como
\[\oint_\mathscr{C} dk_0 \frac{e^{ik_0z^0}}{k_0^2-k^2} = \int_C dk_0 \frac{e^{ik_0z^0}}{k_0^2-k^2} + \int_c dk_0 \frac{e^{ik_0z^0}}{k_0^2-k^2}+\int_{-R}^{R}dk_0 \frac{e^{ik_0z^0}}{k_0^2-k^2} \label{eq:20} \tag{20}\]Donde hemos llamado \(C\) a la curva circular de radio \(R\) y \(c\) a las curvas circulares pequeñas de radio \(\epsilon\). La integral que queremos hallar es el límite cuando \(R\rightarrow \infty\) y \(\epsilon\rightarrow 0\) de la tercera integral del lado derecho de \(\eqref{eq:20}\) . Entonces, veamos el comportamiento de estas integrales en estos límites.
Para la integral en \(C\) hagamos el cambio \(k_0 = Re^{\pm i\theta}\implies dk_0 = \pm iRe^{i\theta}d\theta\) con \(\theta\in [0,2\pi]\).
\[\begin{align} \label{eq:21} \tag{21} \int_C d\theta \pm iR \frac{e^{\pm iRe^{i\theta} z^0}}{R^2 e^{2i\theta}-k^2} \\ \int_C d\theta \pm iR \frac{e^{\pm iR\cos\theta z^0}e^{\mp R\sin\theta z^0}}{R^2 e^{2i\theta}-k^2} \end{align}\]Si elegimos la curva \(\mathscr{C}_U\) elegimos el signo \(+\) y si usamos \(\mathscr{C}_L\) el \(-\) . En el límite \(R\rightarrow \infty\) el factor exponencial \(e^{\mp R\sin\theta }\) decae a cero, entonces se cumple que
\[\lim_{R\rightarrow\infty}\int_C \frac{e^{ik_0z^0}}{k_0^2-k^2} = 0 \label{eq:22} \tag{22}\]Esto tanto para \(z^0>0\) y \(z^0<0\) .
Ahora analicemos las integrales sobre \(c\), es decir, las semicircunferencias de radio \(\epsilon\) que encierran los polos. Al igual que en el caso anterior hagamos un cambio de variables \(k_0 = \epsilon e^{i\theta} \implies dk_0 = i\epsilon e^{i\theta}d\theta\) y veamos el comportamiento cuando \(\epsilon\rightarrow 0\) .
\[\begin{align} \label{eq:23} \tag{23} \int_c d\theta \pm i \epsilon \frac{e^{\pm i \epsilon e^{i\theta} z^0}}{\epsilon ^2 e^{2i\theta}-k^2} \\ \int_c d\theta \pm i \epsilon \frac{e^{\pm i \epsilon \cos\theta z^0}e^{\mp \epsilon\sin\theta z^0}}{\epsilon^2 e^{2i\theta}-k^2} \end{align}\]Es fácil ver que la integral tiende a cero: ֍ De hecho el resultado \(\eqref{eq:22}\) y \(\eqref{eq:24}\) son consecuencia del Lema de Jordan .
\[\lim_{\epsilon\rightarrow 0}\int_C \frac{e^{ik_0z^0}}{k_0^2-k^2} = 0 \label{eq:24} \tag{24}\]Por consiguiente \(\eqref{eq:20}\) quedaría:
\[\oint_{\mathscr{C}} \frac{e^{ik_0z^0}}{k_0^2-k^2} = \lim_{R \rightarrow\infty} \int_{-R}^{R} \frac{e^{ik_0z^0}}{k_0^2-k^2} \label{eq:25} \tag{25}\]Usando el Teorema del Residuo evaluamos la integral de contorno:
\[\begin{align}\label{eq:26} \tag{26} \oint_\mathscr{C} \frac{e^{ik_0z^0}}{k_0^2-k^2} = \oint \frac{e^{ik_0z^0}}{(k_0-k)(k_0+k)} &= 2\pi i \sum_{k_i=+k,-k} Res(e^{ik_0 z},k_i) \\ \nonumber & = 2\pi i \left( \frac{e^{ikz^0}}{2k}-\frac{e^{-ikz^0}}{2k} \right) = -2\pi \frac{\sin(kz^0)}{k} \end{align}\]Llegamos a que:
\[\lim_{R \rightarrow\infty}\int_{-R}^R \frac{e^{ik_0z^0}}{k_0^2-k^2} = -2\pi \frac{\sin(kz^0)}{k} \label{eq:27} \tag{27}\]La función de Green \(\eqref{eq:17}\) ahora se escribe como
\[G(z^\mu)=\frac{1}{2\pi^2}\int d^3k e^{-i\vec{k}\cdot \vec{z}} \frac{\sin(kz^0)}{k} \label{eq:28} \tag{28}\]Sin embargo, si hacemos la integral recorriendo la curva \(\mathscr{C}_L\) la integral daría cero, pues no contiene a ningún polo, en otras palabras, el integrando es una función analítica. Entonces, \(\eqref{eq:28}\) es válido para \(z^0>0\) . ֍ Podemos reunir ambos resultados haciendo uso de la función \(\Theta\) de Heaviside.
The last integral
Para realizar la última integral \(\eqref{eq:28}\) escribimos \(\vec{k}\cdot \vec{z}=kz\cos \theta\) y pasamos a coordenadas esféricas con simétria azimutal: ֍ La simetría azimutal nos saca una constante de \(2\pi\)
\[\begin{align} \label{eq:29} \tag{29} G(z^\mu) &= \frac{2\pi}{2\pi^2}\int_0^\pi d \theta\sin \theta\int_0^\infty dk k^2 e^{-ikz\cos \theta} \frac{\sin(kz^0)}{k}\Theta(z^0) \\ &= \frac{\Theta(z^0)}{\pi} \int_0^\infty dk k \sin(kz^0)\left( \frac{e^{-ikz\cos \theta}}{ikz} \right)_{\theta=0}^{\theta=\pi} \\ &= \frac 2 \pi \Theta(z^0) \frac 1 z \int_0^\infty dk \sin(kz^0)\sin(kz) \\ &= -\frac 1 {4\pi}\Theta(z^0)\frac 1 z \int_{-\infty}^{\infty} dk\left( e^{ik(z^0+z)-e^{ik(z^0-z)}-e^{-ik(z^0-z)}+e^{-ik(z^0+z)}} \right) \\ &=-\frac 1 2 \Theta(z^0)\frac 1 z (2\delta(z^0+z)-2\delta(z^0-z)) \end{align}\]La función \(\delta(z^0+z)\) no tiene soporte cuando \(z^0>0\) entonces por definición debe ser cero. Quedando:
\[G(x^\mu-x'^\mu) = \frac{\delta(x^0-x'^0-|\vec{x}-\vec{x}'|)}{|\vec{x}-\vec{x}'|} \label{eq:30} \tag{30}\]A esta solución de la función de Green se le suele llamar función de Green retardada ya que para evaluar tiempos futuros requiere saber el valor en un tiempo pasado.
Retarded four-potential
Ahora que conocemos la función de Green podemos escribir el cuadripotencial \(\eqref{eq:7}\) como
\[\begin{align} \label{eq:31} \tag{31} A^{\nu}(x^\mu) &= \frac{\mu_0}{4\pi} \int d^4 x' \frac{\delta(x^0-x'^0-|\vec{x}-\vec{x}'|)}{|\vec{x}-\vec{x}'|} J^\nu(x'^\mu) \\ &= \frac{\mu_0}{4\pi} \int d^4 x' \frac{J^\nu(x^0_{ret},x'^i)}{|\vec{x}-\vec{x}'|} \end{align}\]Donde \(x^0_{ret} = x^0-d(\vec{x}-\vec{x}')\) es el tiempo retardado.
Con esto concluye este post. Hemos hallado la función de Green \(\eqref{eq:30}\) para la ecuación de onda que satisface el cuadripotencial y con esto hemos hallado su solución \(\eqref{eq:31}\) . Esto es un resutado importante y representa una piedra angular en el Electromagnetismo ya que permite resolver cualquier problema, siempre y cuando sepamos las distribuciones de carga y corriente.