Introduction to r-simplexes and r-chains
[math Published November 19, 2020
En este post introduciremos las herramientas básicas para la integración de p-formas.
r-simplexes
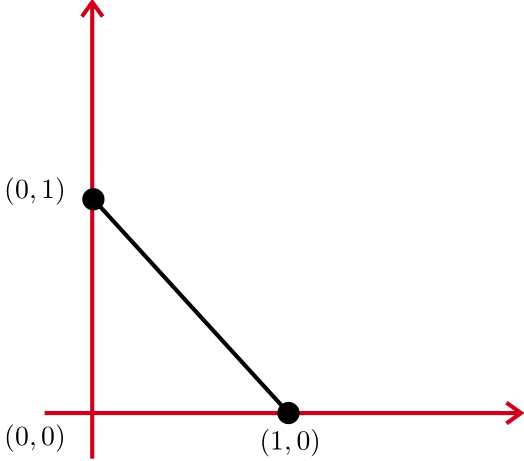
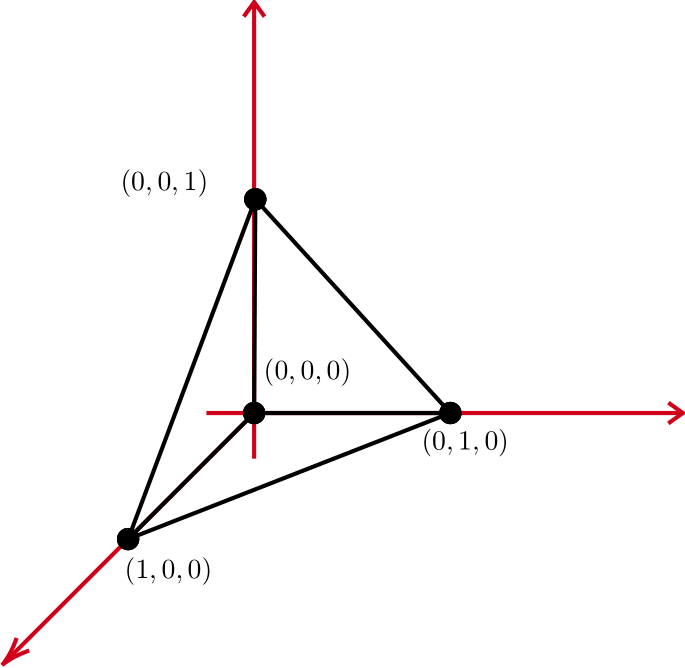
Definimos un r-simplex estándar en un espacio euclídeo como \(\bar\sigma_r=(p_0p_1\cdots r_r)\). Donde \begin{align} p_0 = (0,0,\cdots,0); p_1 = (1,0,\cdots,0); \cdots ; p_r = (0,0,\cdots,1) \end{align}
Por ejemplo, tenemos el 2-simplex como se ve en la figura. Resulta que estos r-simplexes son triángulos para el caso 2 dimensional, son tetrahedros para el caso 3 tridimensional y así.
Sea \(f:\sigma_r\rightarrow M\) un mapeo suave, no necesariamente con una inversa. Denotamos la imagen de \(\sigma_r\) en \(M\) como \(s_r\). Esta imagen se denomina r-simplex singular. Singular, pues no define una triangulación en \(M\). Ahora, consideremos un conjunto de r-simplexes \(\{s_{r,i}\}\) en \(M\). Esto nos permite definir unos objetos llamados r-cadenas o r-chains en inglés de la siguiente forma \begin{equation} c_r = \sum_i a_i s_{r,i} \label{eq:1} \tag{1} \end{equation} Se puede demostrar que estos objetos forma un grupo llamado grupo de r-cadenas denotado por \(C_r(M)\).
Una de las propiedades del mapeo \(f\) es que lleva el borde de \(\sigma_r\) al borde de \(s_r\), es decir, \begin{equation} \text{Si} \ f(\sigma_r) = s_r\implies f(\partial\sigma_r) = \partial s_r \end{equation} Donde el operador de borde es un operador \(\partial:C_r(M)\rightarrow C_{r-1}(M)\) y cumple que \(\partial^2=0\).
Me parece que se puede definir naturalmente un complex al estilo de de Rham donde el homomorfismo entre los espacios sería el operador \(\partial\). Algo como \(C_0(M)\overset{\partial}{\leftarrow}C_1(M)\overset{\partial}{\leftarrow}\cdots\overset{\partial}{\leftarrow}C_r(M)\overset{\partial}{\leftarrow}\cdots\)
Definimos un r-ciclo o r-cycle \(\mathcal c_r\) como aquella r-cadena que satisface \(\partial\mathcal c=0\). También definimos un r-borde o r-boundary a una r-cadena que cumple que \(\mathcal c_r=\partial g_{r+1}\) siempre y cuando exista la r+1-cadena \(g_{r+1}\).
Con estas herramientas ya estamos listos para poder definir una noción de integración de r-formas sobre una r-cadena.