The geometry of Gauge Fields
[math physics Published December 20, 2020
\[\newcommand{\imp}{\implies} % Simbolo de implicacion \newcommand{\supr}[1]{\underset{#1}{\sup}} \newcommand{\mbf}[1]{\mathbf{#1}} % Negrita en modo matemático \newcommand{\lra}{\leftrightarrow} % Flecha derecha e izquierda \newcommand{\h}{\hat} % hat para operadores \newcommand{\red}[1]{\color{red}{#1}} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\blue}[1]{\color{blue}{#1}} \newcommand{\pr}{\partial} % Abreviacion para \partial \newcommand{\cd}{\cdot} % \cdot \newcommand{\cds}{\cdots} % \cdots \newcommand{\inceq}{\subseteq} % incluido e igual \newcommand{\vc}[1]{\vec{#1}} % vector \newcommand{\dg}{^\dagger} \newcommand{\conj}[1]{#1^*} % conjugado \newcommand{\pescalar}[2]{#1\cd #2} % Producto escalar \newcommand{\f}[2]{\frac{#1}{#2}} % Short version for \frac \newcommand{\dott}[1]{\overset{\cdot\cdot}{#1}} % Doble Punto encima (dt) \newcommand{\nab}{\nabla} % Shortcut for nabla %\newcommand{\eval}{\big\rvert} % Raya vertical para indicar evaluación %\newcommand{\deg}[1]{#1^{\circ}} % Grados \newcommand{\la}{\leftarrow} % Leftarrow \newcommand{\mc}[1]{\mathcal{#1}} % Tipografia caligrafia \newcommand{\mf}[1]{\mathfrak{#1}} % Tipografia frakture (gótico) \newcommand{\tf}{\therefore } % Los tres puntitos en triangulo \newcommand{\sder}[2]{\frac{d #1}{d #2}} % Derivada simple de #1 respecto a #2 \newcommand{\der}[3]{\frac{d^{#1}#2}{d #3^{#1}}} % Derivada n-sima de #1 respecto a #2 \newcommand{\sparc}[2]{\frac{\partial #1}{\partial #2}} %Derivadas parciales \newcommand{\parc}[3]{\frac{\partial^{#1}#2}{\partial #3^{#1}}} %Derivada parcial n-esima respecto de #3 \newcommand{\m}[1]{\mathbb{#1}} % Hace una letra R --> \mathbb{R} \newcommand{\inc}{\subset} % Incluido \newcommand{\ndvec}[2]{(#1_1,#1_2,\ldots,#1_{#2})} %Crea un vector #2-dimensional con nombre #1 \newcommand{\ci}{\imath} % Unidad imaginaria \newcommand{\ptodo}{\forall} % Para todo simbolo \newcommand{\me}[1]{#1\m Z} % Multiplos enteros de #1: #1Z. \newcommand{\tq}{\mid} % Simbolo para tal que... \newcommand{\pp}[1]{#1^{\prime\prime}\mkern-1.2mu} %#1´´ \newcommand{\e}[1]{e^{#1}} % Exponencial de #1 \newcommand{\om}{\omega} % Shortcut para omega \newcommand{\Om}{\Omega} % Shortcut para Omega \newcommand{\lam}{\lambda} % Lambda \newcommand{\Lam}{\Lambda} % Lambda mayuscula \newcommand{\al}{\alpha} % alpha \newcommand{\be}{\beta} % beta \newcommand{\gm}{\gamma} % gamma \newcommand{\Gm}{\Gamma} % Gamma \newcommand{\del}{\delta} % Delta \newcommand{\sg}{\sigma} % Sigma \newcommand{\Del}{\Delta} \newcommand{\rel}{\sim} \newcommand{\uvec}[1]{\bm{\hat{\mathbf{#1}}}} % Vector unitario \newcommand{\vct}[1]{\vec{\mathbf{#1}}} \newcommand{\ra}{\rightarrow} \newcommand{\eps}{\epsilon} \newcommand{\ex}{\exists} \newcommand{\bp}[1]{\left(#1\right)} \newcommand{\bb}[1]{\left[#1\right]} \newcommand{\bl}[1]{\left\{#1\right\}} \newcommand{\deld}[1]{\delta^{(3)}(#1)} % Delta de Dirac en 3d \newcommand{\ddrc}[2]{\delta^{(#1)}(#2)} % Delta de Dirac en Nd \newcommand{\lrpr}{\overset{\lra}{\pr}} % left right partial \newcommand{\slashd}{\kern-0.5em\raise0.22ex\hbox{/}} \newcommand{\barra}[1]{\cancel{#1}} \newcommand{\lan}{\langle} \newcommand{\ran}{\rangle}\]
Potenciales de gauge y campos
Comenzamos fijando un grupo de Lie compacto \(G\) (abeliano o no abeliano). Consideraremos su respectiva álgebra de Lie a \(L(G)\). Un campo de gauge es un conjunto de funciones \(A_\mu(x)\) que toman valores en el álgebra \(L(G)\) y donde \(x=(x_1\cdots x_4)\) es un punto en el espacio de Minkowski o en el espacio Euclídeo. Asociado al potencial consideramos al operador
\[\nabla_\mu = \partial_\mu+A_\mu \label{eq:1} \tag{1}\]Este operador actúa sobre una función vectorial \((f_1(x),\cdots,f_m(x))\) siempre y cuando una representación m-dimensional de \(G\) es dada.
Calculando el conmutador de \(\nabla_\mu\) y \(\nabla_\nu\) obtenemos el campo de gauge \(F_{\mu\nu}\), dado por
\[F_{\mu\nu} = [\nabla_\mu,\nabla_\nu] = \partial_\mu A_\nu-\partial_\nu+[A_\mu,A_\nu] \label{eq:2} \tag{2}\]y donde el conmutador \([A_\mu,A_\nu]\) es tomado en el álgebra de \(G\). Lo importante a notar es que para grupos no abelianos, ese conmutador no se anula. Sin embargo, para grupos abelianos como \(U(1)\), este término se anula y obtenemos la relación usual del electromagnetismo.
El hecho de que el potencial de gauge no sea único (electromagnetismo) tiene su contraparte para el caso no abeliano. En este caso, el potencial de gauge transforma como
\[A_\mu\rightarrow g^{-1}A_\mu g+g^{-1}\partial_\mu g \label{eq:3} \tag{3}\]donde la función \(g(x)\) toma valores en el álgebra. El campo de gauge transforma como
\[F_{\mu\nu}\rightarrow g^{-1}F_{\mu\nu}g \label{eq:4} \tag{4}\]Notemos que el potencial de gauge no tranforma homogeneamente como el campo de gauge. Esto quiere decir que \(F_{\mu\nu}\) transforma como un tensor, en cambio, \(A_\mu\) transforma como un objeto afín. Un objeto afín es aquel que no tiene un cero preferido.
Pensemos esto geométricamente . Imaginemos una partícula con estructura interna que está localizada en un punto \(x\in\m R^4\). Por estructura interna podemos referirnos a la carga, spin o un conjunto de estados que están identificados con elementos \(g\) de \(G\). Ahora consideramos al espacio de todos los estados de la partícula y lo denotamos como \(P\). En general el espacio interno \(G_x\) en cada punto distinto, entonces podemos hacer un dibujo como el siguiente
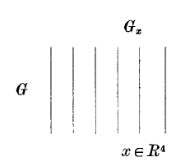
La líneas verticales representan los espacios internos en cada punto de \(x\in\m R^4\) y son llamadas fibras. En ausencia de campos externos consideramos que es posible identificar distintos \(G_x\), de modo que también podemos dibujar unas líneas horizontales como en la siguiente figura
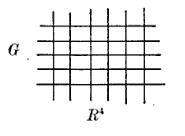
Estas líneas horizontales son llamadas secciones. Si introducimos un campo externo, distorcionamos el alineamiento entre las fibras. Sin embargo, asumimos que aún es posible encontrar un camino definido en \(\m R^4\) que une los puntos \(x\) e \(y\) de modo que se pueda identificar \(G_x\) y \(g_y\). Esta identificación de fibras a lo largo de ciercos caminos es denomina transporte paralelo. En el caso en que se pueda encontrar más de un camino que una los puntos \(x\) e \(y\) no hay razón para estos camino coincidan, pero se asume que se puede obtener el uno del otro por la acción de un elementos del grupo. Esto puede ser visto como un cambio de fase generalizado. Esta cambio de fase se puede pensar como producido por el campo externo.
Consideremos ahora un transporte paralelo infinitesimal, es decir un cambio infinitesimal \(A\) de la fibra \(G_x\) en otra fibra cercana. Esto es lo que se llama una conexión. La curvatura infinitesimal \(F\) depende de dos direcciones en \(x\) y toma valores en el álgebra de Lie de \(G_x\).
Debemos enfatizar que la conexión es un objeto geométrico definido y es más primitivo que la curvatura. Como consecuencia uno debe ver al campo de gauge como un objeto más primitivo que el campo de gauge. Esto tiene consecuencias importantes en el electromagnetismo Ver el efecto Aharonov-Bohm .
Hasta ahora sólo hablamos de fibrados en los cuales el fibrado era el mismo grupo \(G\). Estos son llamados fibrados principales en la geometría diferencial. Sin embargo, en las aplicaciones uno susualmente está interesado en en fibrados en donde la fibra se un espacio vectorial \(C^n\) correspondiente a una representación de \(G\).
Como se puedo leer, este post es más teórico. Nos inicia en el estudio de la geometría de fibrados. En el siguiente post se abordarán las ecuaciones de campo.