Solitons: The kink
[physics math Published March 11, 2021
\[\DeclareMathOperator{\Tr}{Tr} \newcommand{\imp}{\implies} % Simbolo de implicacion \newcommand{\supr}[1]{\underset{#1}{\sup}} \newcommand{\mbf}[1]{\mathbf{#1}} % Negrita en modo matemático \newcommand{\lra}{\leftrightarrow} % Flecha derecha e izquierda \newcommand{\h}{\hat} % hat para operadores \newcommand{\red}[1]{\color{red}{#1}} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\blue}[1]{\color{blue}{#1}} \newcommand{\pr}{\partial} % Abreviacion para \partial \newcommand{\cd}{\cdot} % \cdot \newcommand{\cds}{\cdots} % \cdots \newcommand{\inceq}{\subseteq} % incluido e igual \newcommand{\vc}[1]{\vec{#1}} % vector \newcommand{\dg}{^\dagger} \newcommand{\conj}[1]{#1^*} % conjugado \newcommand{\pescalar}[2]{#1\cd #2} % Producto escalar \newcommand{\f}[2]{\frac{#1}{#2}} % Short version for \frac \newcommand{\dott}[1]{\overset{\cdot\cdot}{#1}} % Doble Punto encima (dt) \newcommand{\nab}{\nabla} % Shortcut for nabla %\newcommand{\eval}{\big\rvert} % Raya vertical para indicar evaluación %\newcommand{\deg}[1]{#1^{\circ}} % Grados \newcommand{\la}{\leftarrow} % Leftarrow \newcommand{\mc}[1]{\mathcal{#1}} % Tipografia caligrafia \newcommand{\mf}[1]{\mathfrak{#1}} % Tipografia frakture (gótico) \newcommand{\tf}{\therefore } % Los tres puntitos en triangulo \newcommand{\sder}[2]{\frac{d #1}{d #2}} % Derivada simple de #1 respecto a #2 \newcommand{\der}[3]{\frac{d^{#1}#2}{d #3^{#1}}} % Derivada n-sima de #1 respecto a #2 \newcommand{\sparc}[2]{\frac{\partial #1}{\partial #2}} %Derivadas parciales \newcommand{\parc}[3]{\frac{\partial^{#1}#2}{\partial #3^{#1}}} %Derivada parcial n-esima respecto de #3 \newcommand{\m}[1]{\mathbb{#1}} % Hace una letra R --> \mathbb{R} \newcommand{\inc}{\subset} % Incluido \newcommand{\ndvec}[2]{(#1_1,#1_2,\ldots,#1_{#2})} %Crea un vector #2-dimensional con nombre #1 \newcommand{\ci}{\imath} % Unidad imaginaria \newcommand{\ptodo}{\forall} % Para todo simbolo \newcommand{\me}[1]{#1\m Z} % Multiplos enteros de #1: #1Z. \newcommand{\tq}{\mid} % Simbolo para tal que... \newcommand{\pp}[1]{#1^{\prime\prime}\mkern-1.2mu} %#1´´ \newcommand{\e}[1]{e^{#1}} % Exponencial de #1 \newcommand{\om}{\omega} % Shortcut para omega \newcommand{\Om}{\Omega} % Shortcut para Omega \newcommand{\lam}{\lambda} % Lambda \newcommand{\Lam}{\Lambda} % Lambda mayuscula \newcommand{\al}{\alpha} % alpha \newcommand{\be}{\beta} % beta \newcommand{\gm}{\gamma} % gamma \newcommand{\Gm}{\Gamma} % Gamma \newcommand{\del}{\delta} % Delta \newcommand{\sg}{\sigma} % Sigma \newcommand{\Del}{\Delta} \newcommand{\rel}{\sim} \newcommand{\uvec}[1]{\bm{\hat{\mathbf{#1}}}} % Vector unitario \newcommand{\vct}[1]{\vec{\mathbf{#1}}} \newcommand{\ra}{\rightarrow} \newcommand{\eps}{\epsilon} \newcommand{\ex}{\exists} \newcommand{\bp}[1]{\left(#1\right)} \newcommand{\bb}[1]{\left[#1\right]} \newcommand{\bl}[1]{\left\{#1\right\}} \newcommand{\deld}[1]{\delta^{(3)}(#1)} % Delta de Dirac en 3d \newcommand{\ddrc}[2]{\delta^{(#1)}(#2)} % Delta de Dirac en Nd \newcommand{\lrpr}{\overset{\lra}{\pr}} % left right partial \newcommand{\slashd}{\kern-0.5em\raise0.22ex\hbox{/}} \newcommand{\barra}[1]{\cancel{#1}} \newcommand{\lan}{\langle} \newcommand{\ran}{\rangle}\]
Teorías de campo en una dimensión espacial proveen un punto de inicio natural para estudiar solitones. Debido a las simplificaciones que resultan de trabajar en una dimensión algunas cuentas se pueden realizar explicitamente. Además, las consideraciones topológicas que juegan un rol importante en la clasificación de solitones en cualquier dimensión son particularmente fáciles de visualizar en teorías de una dimensión.
En este post analizaremos el kink. Yo diría que es el solitón más sencillo de hallar y el más básico.
Kink
El ejemplo clásico de un solitón en un dimensión espacial aparece en un teoría con un solo campo escalar y con la densidad lagrangiana siguiente
\[\mc L = \f 12(\pr_\mu\phi)(\pr^\mu\phi)-V(\phi), \label{eq:1} \tag{1}\]donde el potencial escalar es
\[V(\phi) = \f\lambda 4(\phi^2-v^2)^2. \label{eq:2} \tag{2}\]Donde, además, \(m^2\) y \(\lambda\) son constantes positivas y
\[v = \sqrt{\f{m^2}\lambda} \label{eq:3} \tag{3}\]Notemos que en dos dimensiones espaciotemporales el campo escalar es adimensional, de modo que las constantes de acoplamiento si tienen dimensiones. El parámetro adicional que indica un acoplamiento fuerte o débil es \(\f{\lambda}{m^2}\).
La densidad lagrangiana \(\eqref{eq:1}\) es invariante ante paridad, \(\phi\ra-\phi\). Esta simetría se rompe espontáneamente con \(V(\phi)\) teniendo dos mínimos degenerados en \(\phi = \pm v\). Expandamos el potencial
\[V(\phi) = \f{\lambda}4(\phi^2-v^2)^2 = \f{\lambda\phi^4}4-\f{\lambda\phi^2 v^2}2+\f{\lambda v^4}4.\]El término constante (que no afecta a la dinámica del campo) puede ser ajustado de modo que \(V =0\) en el mínimo. Elijamos alguno de estos mínimos y expandamos el campo alrededor de este mínimo. Por ejemplo, elijamos el vacío \(+v\). Entonces expandamos el campo \(\phi-v\). El término cinético del lagrangiano no se ve afectado pero el potencial arroja un término másico
\[-m^2\phi^2\]Al ser un campo escalar, este término lo interpretamos como una partícula escalar con masa \(\f{M^2}2=m^2\implies M=\sqrt{2}m\).
Las ecuaciones clásicas de Euler-Lagrange para esta teoría son
\[\f{d^2\phi}{d t^2}-\f{d^2\phi}{d x^2}=-\lambda(\phi^2-v^2)\phi \label{eq:4} \tag{4}\]Queremos soluciones estáticas (buscamos un solitón), las cuales satisfacen
\[\f{d^2\phi}{dx^2}-\lambda(\phi^2-v^2)\phi=0 \label{eq:5} \tag{5}\]Esta es una ecuación no lineal y no es obvio que tenga soluciones no singulares a parte de las soluciones triviales \(\phi=\pm v\). Usemos el recién aprendido principio de criticalidad simétrica para probar que de hecho si existen esta soluciones no triviales. Recordemos el principio brevemente
Principio de criticalidad simétrica: Sea \(\phi\) un campo genérico de algún lagrangiano y sea \(S[\phi]\) la acción de la teoría. Sobre la teoría actúa algún grupo de simetría que deja invariante a la acción. Sea \(K\) el conjunto de campos que son invariantes frente a la acción de este grupo. El principio nos dice que si \(\phi_0\in K\) es un punto estacionario de \(S_K[\phi]\) (la acción restringida a \(K\)) entonces automáticamente también es un punto estacionario de la acción total \(S[\phi]\).
En este caso, el grupo de simetría pertinente es \(\{e,P\}\), donde \(P\) que actúa como
\[P\phi(x) = -\phi(-x). \label{eq:6} \tag{6}\]Ya dijimos al inicio que el lagrangiano (por consiguiente la acción) son invariantes frente a la acción de este grupo. Entonces, por el principio anterior podemos a restringirnoas a campos que satisfagan
\[\phi(x) = -\phi(-x). \label{eq:7} \tag{7}\]Basta con encontrar puntos estacionarios de \(S_K[\phi]\) que cumplan \(\eqref{eq:7}\). Está claro, que de existir estas soluciones, estas no son triviales pues los valores de vacío no entran en \(K\). Multiplicando \(\eqref{eq:5}\) por \(\f{d\phi}{dx}\) a ambos lados obtenemos la siguiente ecuación
\[\f{d}{dx}\bb{\f 12\bp{\f{d\phi}{dx}}^2-\f{\lambda}4(\phi^2-v^2)}=0 \label{eq:8} \tag{8}\]La cantidad entre corchetes es independiente de \(x\) y es fácil ver que debe ser cero cuando lo evaluamos en el infinito. Entonces,
\[\f{d\phi}{dx} = \pm\sqrt{\f\lambda 2}(\phi^2-v^2). \label{eq:9} \tag{9}\]Dependiendo de las condiciones de frontera en el infinito, podemos elegir el signo \(+\) o \(-\). De cualquier modo la solución a esta ecuación diferencial es
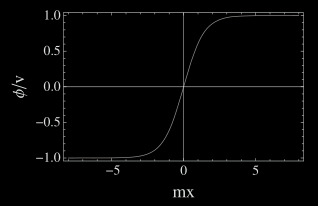
\[\phi(x) = v\tanh\bb{\f m{\sqrt 2}(x-x_0)}, \label{eq:10} \tag{10}\]donde \(x_0\) es una constante de integración. Si fijamos \(x_0\) es claro que la solución satisface \(\eqref{eq:7}\). Esta solución se muestra en la Figura 1 de abajo con \(x_0=0\). Si hubiéramos elegido la solución negativa obtendríamos en antikink
\[\phi(x) = -v\tanh\bb{\f m{\sqrt 2}(x-x_0)}, \label{eq:11} \tag{11}\]
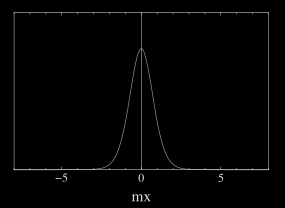
La densidad de energía, mostrada en la Figura 2, es la misma tanto para el kink como para el antikink y está dada por
\[\mc E = \f{m^4}{2\lambda}sech^4\bp{\f{m}{\sqrt 2}x}. \label{eq:12} \tag{12}\]Está concentrada en una región de anchura \(\sim m^{-1}\) alrededor de \(x_0=0\). Fuera de esta región el kink no es distinguible del vacío. Esta localización de la energía sugiere que interpretemos al kink como una especie de partícula.
La masa de esta partícula está dada por la energía total de la solución estática, es decir,
\[M_{cl} = \f{m^4}{2\lambda}\int_{-\infty}^\infty sech^4\bp{\f{m}{\sqrt 2}x} dx = \f{2\sqrt 3}3 \f{m^3}{\lambda}. \label{eq:13} \tag{13}\]Si el kink será interpretado como una partícula, entonces también deberían existir soluciones correspondientes a kinks en movimiento. Obtenemos estas soluciones haciendo una transformación de Lorentz \(x-x_0\ra \gm(x-x_0-ut)\). De esto se obtiene,
\[\phi(x,t) = v\tanh\bb{\f{m}{\sqrt 2}\f{(x-x_0-ut)}{\sqrt{1-u^2}}} \label{eq:14} \tag{14}\]Esto describe un kink en movimiento con velocidad \(u\). La energía de esta solución,
\[E = \int dx\bb{\f 12\bp{\f{d\phi}{dt}}^2+\f 12\bp{\f{d\phi}{dx}}^2+V(\phi)} = \f{M_{cl}}{\sqrt{1-u^2}} \label{eq:15} \tag{15}\]Recordemos que el punto clave para que esta teoría tuviera un solitón es que el potencial tenga vacíos degenerados y que el campo tomara valores distintos en el infinito espacial. Esto establece una relación entre la topología de los vacíos y la topología de los campos en el infinito espacial. El resultado de esta relación es que los solitones son solitones topológicos. Podemos definir una corriente topológica
\[J^\mu_{top} =\f{1}{2v}\eps^{\mu\nu}\pr_\nu\phi, \label{eq:16} \tag{16}\]donde \(\eps^{\mu\nu}=-\eps^{\mu\nu}\) y \(\eps^{01}=1\). La antisimetría de \(\eps\) garantiza que esta corriente tiene divergencia nula. La carga topológica asociada es
\[Q_{top} = \int_{-\infty}^\infty dx J^0 = \f 1{2v}\int_{-\infty}^\infty dx\pr_1\phi = \f 1{2v} [\phi(\infty)-\phi(-\infty)] = \pm 1\]Esta carga está conservada pero no está asociada a una simetría del lagrangiano, en contraste con el Teorema de Noether.
Estos métodos que vimos pueden ser aplicados al caso de un potencial arbitrario \(V(\phi)\) con dos o más mínimos globales degenerados. En general,
\[\f{d\phi}{dx} = \pm\sqrt{2V(\phi)} \label{eq:17} \tag{17}\]Esta última ecuación nos permite derivar una identidad virial:
\[\int_{-\infty}^\infty dx\bb{\f 12\bp{\f{d\phi}{dx}}^2} = \int_{-\infty}^\infty dx V(\phi) \label{eq:18} \tag{18}\]Además, usando esta identidad virial uno puede derivar un cota inferior para la energía \(E\) de cualquier configuración de campos en términos de información topológica (depende sólo de los valores en el infinito). Usemos la siguiente desigualdad
\[\bp{\f 1{\sqrt 2}\phi'\pm\sqrt{V(\phi)}}^2\geq 0\]Expandiendo esta desigualdad e integrando en todo el espacio, obtenemos
\[\int_{-\infty}^\infty\bp{\f 12\phi'+V(\phi)}dx\geq\pm\int_{-\infty}^\infty\sqrt{2V(\phi)}\phi'dx\]Por lo tanto, para campos estáticos
\[E\geq\left\vert \int_{-\infty}^\infty\sqrt{2V(\phi)}\phi'dx\right\vert=\left\vert \int_{\phi_-}^{\phi^+}\sqrt{2V(\phi)}d\phi\right\vert .\]Podemos introducir un superpotencial \(W(\phi)\) tal que \(V(\phi)=\f 12\bp{\f{dW}{d\phi}}^2\), entonces tendríamos
\[E\geq \vert W(\phi_+)-W(\phi_-)\vert \label{eq:19} \tag{19}\]Este tipo de desigualdades se conocen como desigualdades de Bogomolnyi. Es claro que para que se llegue a la igualdad el campo debe ser estático \(\dot\phi=0\) y satisfacer alguna de las llamadas ecuaciones de Bogomolnyi
\[\phi' = \pm\sqrt{2V(\phi)} \label{eq:20} \tag{20}\]Es claro que la solución de kink que obtuvimos satisface la ecuación de Bogomolnyi.
Para concluir este post calculemos la energía de interacción de un par kink-antikink y además mostremos que existe una fuerza atractiva entre ambos. Seguiremos el procedimiento presentado en el libro de Manton y Sutcliffe. Consideremos el momento en el intervalo semi-infinito \(\langle-\infty,b]\) definido como
\[P = -\int_{-\infty}^b\dot\phi\phi' dx \label{eq:21} \tag{21}\]Por lo tanto, la fuerza \(F\) que es la derivada temporal del momento, es
\[\begin{align*} F = \dot P &= -\int_{-\infty}^b (\overset{..}{\phi}\phi'+\dot\phi\dot\phi')dx\\ &= -\int_{-\infty}^b \bb{\bp{\phi''-\f{dV}{d\phi}}\phi'+\dot\phi\dot\phi'}dx\\ &= -\int_{-\infty}^b \bp{\phi''\phi'-\f{dV}{d\phi}\phi'+\dot\phi\dot\phi'}dx\\ &= -\int_{-\infty}^b \bp{\f 12(\phi'^2)'-\f{dV}{dx}+\f 12(\dot\phi^2)'}dx\\ &= -\int_{-\infty}^b \bp{\f 12(\phi'^2+\dot\phi^2)-V}'dx = \bb{-\f 12(\phi'^2+\dot\phi^2)+V}_{-\infty}^b \end{align*}\]Ahora consideremos una par kink-antikink, con el antikink en la posición \(-a\) y el kink en la posición \(a\), donde \(a>>1\). Una configuración de campo que tenga esta forma se puede formar mediante superposición como sigue
\[\phi(x) = \phi_1(x)+\phi_2(x)+1 \label{eq:22} \tag{22}\]La gráfica de esta configuración de campo se muestra en figura (PONER EL GRÁFICO). En el intervalo \(-a<<b<<a\) la configuración de campo alcanza el valor de \(-1\). Entonces, \(1+\phi_2\approx 0\). Podemos usar este hecho a nuestro favor para no tener que calcular todo a la fuerza. El campo \(V(\phi)\) se puede linealizar como sigue
\[V(\phi) = V(\phi_1+\phi_2+1) \approx V(\phi)+(1+\phi_2)\f{dV}{d\phi_1} \label{eq:23} \tag{23}\]También podemos tirar términos cuadráticos en \(\phi_2\) y su derivada espacial. Con esta linealización la fuerza toma la forma
\[F = \bb{-\f{\phi_1'^2}{2}+V(\phi_1)-\phi_1'\phi_2'+(1+\phi_2)\f{dV}{d\phi_1}}_{-\infty}^b\]Podemos usar el hecho de que los campos \(\phi_1,\phi_2\) satisface la ecuación de Bogomolnyi \(\eqref{eq:20}\) para reducir la expresión anterior
\[F = \bb{-\phi_1'\phi_2'+(1+\phi_2)\phi_1''}_{-\infty}^b \label{eq:24} \tag{24}\]Es fácil ver por la forma funcional de \(\phi_1\) y \(\phi_2\) que sus derivadas se anulan en el infinito, de modo que sólo tenemos contribución del límite superior. Para evaluar este límite usemos las formas asintóticas de los campos
\[\phi_1(x)\sim -1+2ee^{-2(x+a)} \ , \ \ \ \phi_2(x)\sim -1+2e^{2(x-a)} \label{eq:25} \tag{25}\]Reemplazando en \(\eqref{eq:24}\) obtenemos una expresión para la fuerza
\[F = 32e^{-2R} = \f{dE_{int}}{dR} \label{eq:26}, \tag{26}\]donde definimos la distancia de separación kink-antikink \(R=2a\). Integrando, obtenemos la energía de interacción
\[E_{int} = -16e^{-2R} \label{eq:27} \tag{27}\]que es negativa y decrece con la distancia de separación, indicando una fuerza atractiva entre kink y antikink.