Solitons: Generalizations of the kink
[physics math Published April 02, 2021
\[\DeclareMathOperator{\Tr}{Tr} \newcommand{\imp}{\implies} % Simbolo de implicacion \newcommand{\supr}[1]{\underset{#1}{\sup}} \newcommand{\mbf}[1]{\mathbf{#1}} % Negrita en modo matemático \newcommand{\lra}{\leftrightarrow} % Flecha derecha e izquierda \newcommand{\h}{\hat} % hat para operadores \newcommand{\red}[1]{\color{red}{#1}} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\blue}[1]{\color{blue}{#1}} \newcommand{\pr}{\partial} % Abreviacion para \partial \newcommand{\cd}{\cdot} % \cdot \newcommand{\cds}{\cdots} % \cdots \newcommand{\inceq}{\subseteq} % incluido e igual \newcommand{\vc}[1]{\vec{#1}} % vector \newcommand{\dg}{^\dagger} \newcommand{\conj}[1]{#1^*} % conjugado \newcommand{\pescalar}[2]{#1\cd #2} % Producto escalar \newcommand{\f}[2]{\frac{#1}{#2}} % Short version for \frac \newcommand{\dott}[1]{\overset{\cdot\cdot}{#1}} % Doble Punto encima (dt) \newcommand{\nab}{\nabla} % Shortcut for nabla %\newcommand{\eval}{\big\rvert} % Raya vertical para indicar evaluación %\newcommand{\deg}[1]{#1^{\circ}} % Grados \newcommand{\la}{\leftarrow} % Leftarrow \newcommand{\mc}[1]{\mathcal{#1}} % Tipografia caligrafia \newcommand{\mf}[1]{\mathfrak{#1}} % Tipografia frakture (gótico) \newcommand{\tf}{\therefore } % Los tres puntitos en triangulo \newcommand{\sder}[2]{\frac{d #1}{d #2}} % Derivada simple de #1 respecto a #2 \newcommand{\der}[3]{\frac{d^{#1}#2}{d #3^{#1}}} % Derivada n-sima de #1 respecto a #2 \newcommand{\sparc}[2]{\frac{\partial #1}{\partial #2}} %Derivadas parciales \newcommand{\parc}[3]{\frac{\partial^{#1}#2}{\partial #3^{#1}}} %Derivada parcial n-esima respecto de #3 \newcommand{\m}[1]{\mathbb{#1}} % Hace una letra R --> \mathbb{R} \newcommand{\inc}{\subset} % Incluido \newcommand{\ndvec}[2]{(#1_1,#1_2,\ldots,#1_{#2})} %Crea un vector #2-dimensional con nombre #1 \newcommand{\ci}{\imath} % Unidad imaginaria \newcommand{\ptodo}{\forall} % Para todo simbolo \newcommand{\me}[1]{#1\m Z} % Multiplos enteros de #1: #1Z. \newcommand{\tq}{\mid} % Simbolo para tal que... \newcommand{\pp}[1]{#1^{\prime\prime}\mkern-1.2mu} %#1´´ \newcommand{\e}[1]{e^{#1}} % Exponencial de #1 \newcommand{\om}{\omega} % Shortcut para omega \newcommand{\Om}{\Omega} % Shortcut para Omega \newcommand{\lam}{\lambda} % Lambda \newcommand{\Lam}{\Lambda} % Lambda mayuscula \newcommand{\al}{\alpha} % alpha \newcommand{\be}{\beta} % beta \newcommand{\gm}{\gamma} % gamma \newcommand{\Gm}{\Gamma} % Gamma \newcommand{\del}{\delta} % Delta \newcommand{\sg}{\sigma} % Sigma \newcommand{\Del}{\Delta} \newcommand{\rel}{\sim} \newcommand{\uvec}[1]{\bm{\hat{\mathbf{#1}}}} % Vector unitario \newcommand{\vct}[1]{\vec{\mathbf{#1}}} \newcommand{\ra}{\rightarrow} \newcommand{\eps}{\epsilon} \newcommand{\ex}{\exists} \newcommand{\bp}[1]{\left(#1\right)} \newcommand{\bb}[1]{\left[#1\right]} \newcommand{\bl}[1]{\left\{#1\right\}} \newcommand{\deld}[1]{\delta^{(3)}(#1)} % Delta de Dirac en 3d \newcommand{\ddrc}[2]{\delta^{(#1)}(#2)} % Delta de Dirac en Nd \newcommand{\lrpr}{\overset{\lra}{\pr}} % left right partial \newcommand{\slashd}{\kern-0.5em\raise0.22ex\hbox{/}} \newcommand{\barra}[1]{\cancel{#1}} \newcommand{\lan}{\langle} \newcommand{\ran}{\rangle}\]
Las soluciones kink que hemos obtenido en los posts anteriores pueden ser embebidas trivialmente en un teoría de mayor dimensión: simplemente la solución será independiente de las demás variables. Sin embargo, la energía de esta solución se hace infinita pues tiene una extensión infinita en las otras direcciones. Aún así, estas soluciones tienen energía por unidad de área finita. Este tipo de solución son conocidas como domain walls y son de importancia en aplicaciones en materia condensada y en cosmología.
Potenciales con más de dos mínimos degenerados aislados
Para una teoría en la cual el potencial \(V\) tiene más de dos mínimos degenerados aislados un fenómeno interesante puede ocurrir para los domain walls, esto es, pueden existir soluciones estáticas en la cual tres o más domain walls se juntan en lo que se denomina una juntura. La familia más simple de teorías con soluciones de este tipo tiene un campo escalar complejo \(\phi\) y una densidad lagrangiana como sigue
\[\mc L = \f 14\pr_\mu\bar\phi\pr^\mu\phi-\vert W'(\phi)\vert^2, \label{eq:1} \tag{1}\]donde \(W(\phi)\) es una función holomorfa de \(\phi\), conocido como superpotencial. En la presente discusión nos restringimos a configuraciones estáticas y consideramos campos que son independientes de \(x^3\), de modo que tenemos un modelo en el plano \((x_1,x_2)\) efectivamente.
Sea \(z\) la coordenada compleja en el plano, \(z=x^1+\ci x^2\), y denotemos las derivadas parciales con respecto a \(z\) y \(\bar z\) como \(\pr_z\) y \(\pr_{\bar z}\) respectivamente,
\[\pr_z = \f 12(\pr_1-\ci\pr_2), \ \ \pr_{\bar z}=\f 12(\pr_1+\ci\pr_2) \label{eq:2} \tag{2}\]La energía de la solución estática es
\[E = \int\bb{\f 12(\pr_1\phi)^2+\f 12(\pr_2\phi)^2+\vert W'(\phi)\vert^2}d^2 x \label{eq:3} \tag{3}\]También la podemos escribir e función de la variable compleja \(z\) de la siguiente forma
\[E = \int\bb{\f 12(\vert\pr_z\phi\vert^2+\vert\pr_{\bar z}\phi\vert^2)+\vert W'(\phi)\vert^2} d^2x \label{eq:4} \tag{4}\]La variación de esta energía produce la siguiente ecuación de segundo orden
\[\pr_{\bar z}\pr_z\phi = \overline{W''(\phi)}W'(\phi) \label{eq:5} \tag{5}\]Existe una familia monoparamétrica de ecuaciones de Bogomolnyi asociadas con este sistema, dadas por
\[\pr_z\phi = e^{i\al}\overline{W'(\phi)}, \label{eq:6} \tag{6}\]donde \(\al\) es una constante de fase. Es fácil verificar que las soluciones de esta ecuación de Bogomolnyi satisfacen la ecuación diferencial de segundo orden \(\eqref{eq:5}\). Veámoslo de manera explícita,
\[\pr_{\bar z}\pr_z\phi = \pr_{\bar z}(e^{i\al}\overline{W'(\phi)}) = e^{i\al}\overline{W''(\phi)}\pr_{\bar z}\bar\phi = \overline{W''(\phi)}W'(\phi) \label{eq:7} \tag{7}\]Nótese que la fase \(\al\) puede ser removida haciendo una rotación de fase en la coordenada \(z\), lo que corresonde a una rotación en el plano. Campos que satisfacen las ecuaciones de anti-Bogomolnyi \(\pr_{\bar z}\phi=e^{i\be}\overline{W'(\phi)}\) también satisfacen la ecuación \(\eqref{eq:5}\).
Para obtener soluciones a las ecuaciones de Bogomolnyi que representen una juntura domain wall necesitamos un potencial que tenga al menos tres vacíos distintos. Con esto en mente, consideremos el siguiente superpotencial cuártico
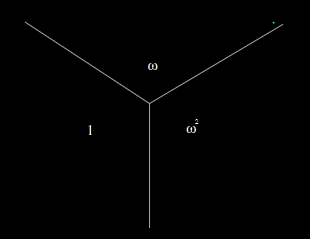
\[W(\phi) = \phi-\f 14\phi^4 \label{eq:8} \tag{8}\]Los mínimos de \(\vert W'(\phi)\vert^2 = \vert 1-\phi^3\vert^2\) son tres raíces de la unidad \(\phi_0=1,\om,\om^2\), donde \(\om=e^{2\pi\ci/3}\). Es fácil visualizar al plano dividido en tres sectores simétricos como se muestra en la Figura 1