Solitons: Vortices in the Ginzburg-Landau Theory - the global theory case
[physics Published April 29, 2021
\[\DeclareMathOperator{\Tr}{Tr} \newcommand{\imp}{\implies} % Simbolo de implicacion \newcommand{\supr}[1]{\underset{#1}{\sup}} \newcommand{\mbf}[1]{\mathbf{#1}} % Negrita en modo matemático \newcommand{\lra}{\leftrightarrow} % Flecha derecha e izquierda \newcommand{\h}{\hat} % hat para operadores \newcommand{\red}[1]{\color{red}{#1}} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\blue}[1]{\color{blue}{#1}} \newcommand{\pr}{\partial} % Abreviacion para \partial \newcommand{\cd}{\cdot} % \cdot \newcommand{\cds}{\cdots} % \cdots \newcommand{\inceq}{\subseteq} % incluido e igual \newcommand{\vc}[1]{\vec{#1}} % vector \newcommand{\dg}{^\dagger} \newcommand{\conj}[1]{#1^*} % conjugado \newcommand{\pescalar}[2]{#1\cd #2} % Producto escalar \newcommand{\f}[2]{\frac{#1}{#2}} % Short version for \frac \newcommand{\dott}[1]{\overset{\cdot\cdot}{#1}} % Doble Punto encima (dt) \newcommand{\nab}{\nabla} % Shortcut for nabla %\newcommand{\eval}{\big\rvert} % Raya vertical para indicar evaluación %\newcommand{\deg}[1]{#1^{\circ}} % Grados \newcommand{\la}{\leftarrow} % Leftarrow \newcommand{\mc}[1]{\mathcal{#1}} % Tipografia caligrafia \newcommand{\mf}[1]{\mathfrak{#1}} % Tipografia frakture (gótico) \newcommand{\tf}{\therefore } % Los tres puntitos en triangulo \newcommand{\sder}[2]{\frac{d #1}{d #2}} % Derivada simple de #1 respecto a #2 \newcommand{\der}[3]{\frac{d^{#1}#2}{d #3^{#1}}} % Derivada n-sima de #1 respecto a #2 \newcommand{\sparc}[2]{\frac{\partial #1}{\partial #2}} %Derivadas parciales \newcommand{\parc}[3]{\frac{\partial^{#1}#2}{\partial #3^{#1}}} %Derivada parcial n-esima respecto de #3 \newcommand{\m}[1]{\mathbb{#1}} % Hace una letra R --> \mathbb{R} \newcommand{\inc}{\subset} % Incluido \newcommand{\ndvec}[2]{(#1_1,#1_2,\ldots,#1_{#2})} %Crea un vector #2-dimensional con nombre #1 \newcommand{\ci}{\imath} % Unidad imaginaria \newcommand{\ptodo}{\forall} % Para todo simbolo \newcommand{\me}[1]{#1\m Z} % Multiplos enteros de #1: #1Z. \newcommand{\tq}{\mid} % Simbolo para tal que... \newcommand{\pp}[1]{#1^{\prime\prime}\mkern-1.2mu} %#1´´ \newcommand{\e}[1]{e^{#1}} % Exponencial de #1 \newcommand{\om}{\omega} % Shortcut para omega \newcommand{\Om}{\Omega} % Shortcut para Omega \newcommand{\lam}{\lambda} % Lambda \newcommand{\Lam}{\Lambda} % Lambda mayuscula \newcommand{\al}{\alpha} % alpha \newcommand{\be}{\beta} % beta \newcommand{\gm}{\gamma} % gamma \newcommand{\Gm}{\Gamma} % Gamma \newcommand{\del}{\delta} % Delta \newcommand{\sg}{\sigma} % Sigma \newcommand{\Del}{\Delta} \newcommand{\rel}{\sim} \newcommand{\uvec}[1]{\bm{\hat{\mathbf{#1}}}} % Vector unitario \newcommand{\vct}[1]{\vec{\mathbf{#1}}} \newcommand{\ra}{\rightarrow} \newcommand{\eps}{\epsilon} \newcommand{\ex}{\exists} \newcommand{\bp}[1]{\left(#1\right)} \newcommand{\bb}[1]{\left[#1\right]} \newcommand{\bl}[1]{\left\{#1\right\}} \newcommand{\deld}[1]{\delta^{(3)}(#1)} % Delta de Dirac en 3d \newcommand{\ddrc}[2]{\delta^{(#1)}(#2)} % Delta de Dirac en Nd \newcommand{\lrpr}{\overset{\lra}{\pr}} % left right partial \newcommand{\slashd}{\kern-0.5em\raise0.22ex\hbox{/}} \newcommand{\barra}[1]{\cancel{#1}} \newcommand{\lan}{\langle} \newcommand{\ran}{\rangle}\]
La teoría de campo más básica que presenta soluciones solitónicas de tipo vórtice es una teoría con un campo escalar complejo
\[\phi = \phi_1+i\phi_2\]que además tiene una simetría interna \(U(1)\) dada por \(\phi(x)\ra e^{i\al}\phi(x)\) y que vive en un espacio de dimensión $n=2$. Por supuesto, como es muy sabido el parámetro \(\al\) puede ser constante o puede depender de las coordenadas. En el primer caso, diremos que se trata de una simetría global y por consiguiente la teoría se llamará teoría global. En el segundo caso, debemos insertar campos auxiliares, más conocidos como campos de gauge, para mantener esta simetría. En este caso diremos que la teoría está gaugeada.
Funcional de energía de Ginzburg-Landau
Los solitones son, por definición, soluciones de las ecuaciones de campo estáticas. Esto nos permite sólo concentrarnos en buscar puntos críticos de la energía para encontrar dichas soluciones. Por este motivo, definimos el funcional de energía de Ginzburg-Landau como sigue
\[V[\phi] = \f 12\int d^2x\bp{\nabla\phi\cd\nabla\phi+U(\phi\bar\phi)} \label{eq:1} \tag{1}\]Necesitamos que \(U\) dependa sólo de el módulo del campo para mantener la simetría \(U(1)\). Este potencial a lo mucho debe ser de orden cuártico o séxtico en $\vert \phi\vert$. Tomaremos el conocido potencial cuártico de Higgs
\[U(\phi\bar\phi) = \f{\lambda}8(m^2-\vert\phi\vert^2)^2 \label{eq:2} \tag{2}\]donde \(\lambda>0\) es una constante.
Para propósitos de cálculo que veremos más adelante, definiremos un producto escalar. El plano \(\m R^2\) tiene el producto escalar usual, pero bajo la identificación \(\m R^2\simeq\m C\), este producto escalar se transforma en
\[(a,b) = \f{a\bar b+\bar a b}2 \label{eq:3} \tag{3}\]Este producto tiene una propiedades interesantes: para \(a,b\in\m R\)
\[\begin{align*} (a,b) &= (ia,ib) = ab\\ (a,ib) &= (ia,b) = 0 \end{align*}\]Entonces, podemos reescribir el funcional \(\eqref{eq:1}\) de la siguiente manera
\[V[\phi] = \f 12\int d^2x\bp{(\nabla\phi,\nabla\phi)+\f{\lambda}4(1-(\phi,\phi))^2} \label{eq:4} \tag{4}\]De esta forma es realmente fácil ver que el funcional es invariante \(U(1)\). Entonces, este funcional corresponde a la Teoría de Ginzburg-Landau global.
Las ecuaciones de Euler-Lagrange para esta teoría son
\[-\Delta\phi = \f{\lambda}2(1-\vert\phi\vert^2)\phi \label{eq:5} \tag{5}\]Los mínimos del potencial son los campos de la forma \(\vert\phi_0\vert=1\implies \phi_0 = e^{i\al}\), donde \(\al\) es función de las coordenadas. Estos mínimos del potencial rompen la simetría \(U(1)\).
Si queremos soluciones tipo vorticiales queremos que el campo \(\phi\) sea no trivial en el infinito, para esto pedimos que \(\phi_\infty=\phi_0\). Esta no es una condición impuesta, si no que puede explicarse si se pide que la energía \(V[\phi]\) sea finita cuando \(\vert \vct x\vert\ra\infty\). Otra cosa que queremos que cumpla el campo en el infinito es que sea univaluada, esto impone condiciones sobre la función \(\al\). Para analizar estas condiciones, pasemos a coordenadas polares:
\[V[\phi] = \f 12\int_0^\infty\int_0^{2\pi}\bp{\pr_\rho\bar\phi\pr_\rho\phi+\f 1{\rho^2}\pr_\theta\bar\phi\pr_\theta+\f{\lambda}4(1-\vert\phi\vert^2)^2}\rho d\rho d\theta \label{eq:6} \tag{6}\]La condición de energía finita en \(\vert\vct x\vert\ra\infty\) implica que
\[\begin{align*} Lim_{\rho\ra\infty}\vert\phi\vert &= 1\\ Lim_{\rho\ra\infty}\pr_\rho\phi &=0 \end{align*}\]La primera condición implica que \(\phi_\infty = \phi_0 = e^{i\al(r,\theta)}\), mientras que la segunda condición implica que \(\al(r,\theta) = \al(\theta)\). Esto junto con la condición de que \(\phi_\infty\) sea una función univaluada implican que
\[\al(2\pi) = \al(0)+2\pi N, \ \ \ N\in\m Z\]Dado este comportamiento del campo en el infinito podemos plantear un ansatz para la solución
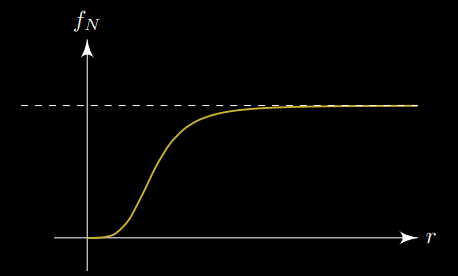
\[\phi(r,\theta) = f_N(r)e^{iN\theta} \label{eq:7} \tag{7}\]Donde además requerimos que \(f_N(r)\ra 1\) cuando \(r\ra\infty\). También notemos que para que la solución sea suave requerimos que \(f_N(0)=0\).
Esta solución es lo que se conoce como un vórtice de Ginzburg-Landau. Una imagen la solución radial se puede ver en Figura 1
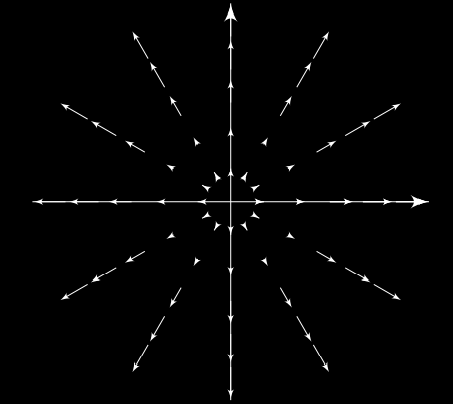
Una mejor forma de visualizar a la solución vorticial es graficandolo como si fuera una campo vectorial en \(\m C\), esto se ve en Figura 2.
Calculemos la cantidad \((i\phi,d\phi)\):
\[(i\phi,d\phi) = (i\phi_1-\phi_2,d\phi_1+id\phi_2)=\phi_1d\phi_2-\phi_2 d\phi_1\]Recordemos la ecuación de continuidad de mecánica cuántica
\[\f 12\pr_t(\vert\phi\vert^2)+\f 1{2m}\nabla\cd (\phi\nabla\bar\phi-\bar\phi\nabla\phi) = 0\]Donde la corriente era $\vct j = \phi\nabla\bar\phi-\bar\phi\nabla\phi$. Entonces, comparando ambas expresiones podemos asociar al término \((i\phi,d\phi)\) con una corriente topológica. Calculemos la corriente para nuestra solución vorticial
\[\begin{align*} (i\phi,d\phi) &= (if_Ne^{iN\theta},(df_N)e^{iN\theta}+if_N N e^{iN\theta}d\theta)\\ &= (if_N,df_N+if_N Nd\theta)\\ &= f_N^2 Nd\theta \end{align*}\]Graficando esta corriente como un campo vectorial en \(\m C\) se obtiene la Figura 3
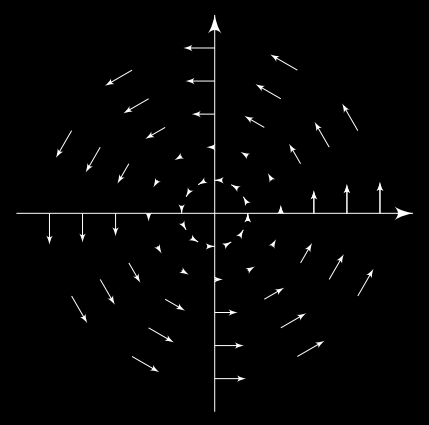
Calculemos la carga topológica definida como
\[\begin{align*} Q &= \f 1\pi\int_D d\phi_1\wedge d\phi_2 = \f 1\pi\int_D d(\phi_1 d\phi_2) = \f 1{2\pi}\int_D d(\phi_1d\phi_2-\phi_2d\phi_1)\\ &= \f 1{2\pi}\int_D d(i\phi,d\phi)\\ &= \f 1{2\pi}\oint_{\pr D}(i\phi,d\phi) \end{align*}\]Donde \(D\) es cualquier región simplemente conexa del plano \(\m R^2\). En particular podemos elegir un disco de radio muy grande \(R\).
Para nuestro caso
\[Q = \f 1{2\pi}lim_{R\ra\infty}\oint (i\phi,d\phi) = \f 1{2\pi}lim_{R\ra\infty}\oint f_N^2 N d\theta = N\]pues \(f_N\ra 1\).
Todo bien con esta teoría pero tiene un problema: la energia es infinita. De hecho, la energía diverge logarítmicamente. Y debe ser así por consecuencia del Teorema de Derrick. Según el teorema no podemos tener soluciones solitónicas en dos dimensiones que tengan energía finita para una teoría global. Para superar este obstáculo insertamos los campos de gauge, que es de lo que tratará el siguiente post.