Solitons: Vortices in the Ginzburg-Landau Theory - the gauged theory case
[physics Published May 15, 2021
\[\DeclareMathOperator{\Tr}{Tr} \newcommand{\imp}{\implies} % Simbolo de implicacion \newcommand{\supr}[1]{\underset{#1}{\sup}} \newcommand{\mbf}[1]{\mathbf{#1}} % Negrita en modo matemático \newcommand{\lra}{\leftrightarrow} % Flecha derecha e izquierda \newcommand{\h}{\hat} % hat para operadores \newcommand{\red}[1]{\color{red}{#1}} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\blue}[1]{\color{blue}{#1}} \newcommand{\pr}{\partial} % Abreviacion para \partial \newcommand{\cd}{\cdot} % \cdot \newcommand{\cds}{\cdots} % \cdots \newcommand{\inceq}{\subseteq} % incluido e igual \newcommand{\vc}[1]{\vec{#1}} % vector \newcommand{\dg}{^\dagger} \newcommand{\conj}[1]{#1^*} % conjugado \newcommand{\pescalar}[2]{#1\cd #2} % Producto escalar \newcommand{\f}[2]{\frac{#1}{#2}} % Short version for \frac \newcommand{\dott}[1]{\overset{\cdot\cdot}{#1}} % Doble Punto encima (dt) \newcommand{\nab}{\nabla} % Shortcut for nabla %\newcommand{\eval}{\big\rvert} % Raya vertical para indicar evaluación %\newcommand{\deg}[1]{#1^{\circ}} % Grados \newcommand{\la}{\leftarrow} % Leftarrow \newcommand{\mc}[1]{\mathcal{#1}} % Tipografia caligrafia \newcommand{\mf}[1]{\mathfrak{#1}} % Tipografia frakture (gótico) \newcommand{\tf}{\therefore } % Los tres puntitos en triangulo \newcommand{\sder}[2]{\frac{d #1}{d #2}} % Derivada simple de #1 respecto a #2 \newcommand{\der}[3]{\frac{d^{#1}#2}{d #3^{#1}}} % Derivada n-sima de #1 respecto a #2 \newcommand{\sparc}[2]{\frac{\partial #1}{\partial #2}} %Derivadas parciales \newcommand{\parc}[3]{\frac{\partial^{#1}#2}{\partial #3^{#1}}} %Derivada parcial n-esima respecto de #3 \newcommand{\m}[1]{\mathbb{#1}} % Hace una letra R --> \mathbb{R} \newcommand{\inc}{\subset} % Incluido \newcommand{\ndvec}[2]{(#1_1,#1_2,\ldots,#1_{#2})} %Crea un vector #2-dimensional con nombre #1 \newcommand{\ci}{\imath} % Unidad imaginaria \newcommand{\ptodo}{\forall} % Para todo simbolo \newcommand{\me}[1]{#1\m Z} % Multiplos enteros de #1: #1Z. \newcommand{\tq}{\mid} % Simbolo para tal que... \newcommand{\pp}[1]{#1^{\prime\prime}\mkern-1.2mu} %#1´´ \newcommand{\e}[1]{e^{#1}} % Exponencial de #1 \newcommand{\om}{\omega} % Shortcut para omega \newcommand{\Om}{\Omega} % Shortcut para Omega \newcommand{\lam}{\lambda} % Lambda \newcommand{\Lam}{\Lambda} % Lambda mayuscula \newcommand{\al}{\alpha} % alpha \newcommand{\be}{\beta} % beta \newcommand{\gm}{\gamma} % gamma \newcommand{\Gm}{\Gamma} % Gamma \newcommand{\del}{\delta} % Delta \newcommand{\sg}{\sigma} % Sigma \newcommand{\Del}{\Delta} \newcommand{\rel}{\sim} \newcommand{\uvec}[1]{\bm{\hat{\mathbf{#1}}}} % Vector unitario \newcommand{\vct}[1]{\vec{\mathbf{#1}}} \newcommand{\ra}{\rightarrow} \newcommand{\eps}{\epsilon} \newcommand{\ex}{\exists} \newcommand{\bp}[1]{\left(#1\right)} \newcommand{\bb}[1]{\left[#1\right]} \newcommand{\bl}[1]{\left\{#1\right\}} \newcommand{\deld}[1]{\delta^{(3)}(#1)} % Delta de Dirac en 3d \newcommand{\ddrc}[2]{\delta^{(#1)}(#2)} % Delta de Dirac en Nd \newcommand{\lrpr}{\overset{\lra}{\pr}} % left right partial \newcommand{\slashd}{\kern-0.5em\raise0.22ex\hbox{/}} \newcommand{\barra}[1]{\cancel{#1}} \newcommand{\lan}{\langle} \newcommand{\ran}{\rangle}\]
En este post vamos a hablar sobre las soluciones del tipo vórtice para la teoría de Ginzburg-Landau gauge. Esto es, vamos a agregar campos de gauge para así poder esquivar el Teorema de Derrick y obtener soluciones con energía finita. Esta teoría es más conocida como el modelo abeliano de Higgs.
Funcional de energía
Vamos a agregar un campo de gauge \(A = A_1 dx^1+A_2 dx^2\) al funcional de energía de Landau (ver post anterior) usando el acoplamiento mínimo
\[D\phi = D_A\phi = d\phi-iA\phi \label{eq:1} \tag{1}\]El funcional de Landau en la teoría gauge es
\[V_\lambda = \f 12\int\bp{B^2+\overline{D_i\phi}D_i\phi+\f{\lambda}4(m^2-\bar\phi\phi)^2}d^2x \label{eq:2} \tag{2}\]Donde \(Bdx^1\wedge dx^2=dA\) o \(B=\pr_1 A_2-\pr_2 A_1\).
Consideremos una transformación de gauge local
y comprobemos que el funcional \(V_\lambda\) es invariante de gauge. Esto es claro, el término \(\bar\phi\phi\) es invariante de gauge, comprobemos que \(B\) es invariante de gauge:
\[B dx^1\wedge dx^2 = dA\ra B dx^1\wedge dx^2 = d(A+d\chi) = dA+d^2\chi = dA\]pues \(d^2=0\). Por último, el término \(\overline{D_i\phi}D_i\phi\)
\[\begin{align*} D\phi = d\phi-iA\phi&\ra (d-i(A+d\chi))e^{i\chi}\phi(x)=ie^{i\chi}d\chi\phi+e^{i\chi}d\phi-iAe^{i\chi}\phi-ie^{i\chi}d\chi\phi\\ &= e^{i\chi}(d-iA)\phi = e^{i\chi}D\phi \end{align*}\]Entonces, \(\overline{D\phi}\ra e^{-i\chi}\overline{D\phi}\). Con estos resultados, resulta fácil ver que \(\overline{D_i\phi}D_i\phi\) es invariante gauge.
En dos dimensiones espaciales, el tensor de campo electromagnético \(f_{\mu\nu}\) sólo tiene tres componentes independientes. Una es el campo magnético \(B\) que ya definimos antes, y las otras dos corresponden a componentes del campo eléctrico \(E_1 = \pr_0A_1-\pr_1A_0\) y \(E_2=\pr_0 A_2-\pr_2 A_0\). Pero, se preguntarán, por qué no aparecen las componentes del campo eléctrico en el funcional. La respuesta es sencilla, ya que el funcional es un funcional de energía, sólo estamos considerando soluciones estáticas, es decir, que las derivadas temporales se hacen cero.
Las ecuaciones de campo se pueden hallar fácilmente y estas son
\[\begin{align*} D_iD_i\phi+\f{\lambda}2(m^2-\bar\phi\phi)\phi &= 0\\ \pr_2 B &= (i\phi,D_1\phi) = \f i2(\bar\phi D_1\phi-\phi \overline{D_1\phi})\\ -\pr_1 B &= (i\phi,D_2\phi) = \f i2(\bar\phi D_2\phi-\phi \overline{D_2\phi}) \end{align*}\]Las dos últimas ecuaciones se pueden juntar en una sóla
\[\eps_{ij}\pr_j B+(i\phi,D_i\phi) =0\]Esta última ecuación es como una versión bidimensional de la Ley de Ampere \(\nabla\times B=J\), entonces el segundo término puede interpretarse como una corriente en el plano.
El vacío en esta teoría es único y la energía se minimiza cuando \(\phi=\vert m\vert\), \(D_i\phi=0\) y \(B=0\) en todo punto. La primera condición implica que \(\phi(x)=me^{i\chi(x)}\) y la última condición implica que el campo de gauge debe ser un gauge puro
\[\begin{align*} A_i(x) = \pr_i\al(x) \end{align*}\]La segunda condición se cumple entonces cuando
\[\begin{align*} D_i\phi = (\pr_i-A_i)me^{i\chi(x)} = im(\pr_i\chi-\pr_i\al)e^{i\chi}=0\\ \implies \pr_i(\chi-\al) =0 \end{align*}\]Esto implica que \(\al=\chi+\text{cte.}\). Entonces, un vacío es de la forma
\[\phi = me^{i\chi}, \ \ A_i = \pr_i\chi \label{eq:3} \tag{3}\]Podemos elegir el gauge \(\chi=0\), entonces tendríamos que una configuración de vacío es \((\phi,A)=(m,0)\).
Queremos obtener una versión en cordenadas polares de las ecuaciones de movimiento, para esto hacemos el siguiente cambio de variables
\[x^1 = \rho\cos\theta, \ \ x^2 = \rho\sin\theta\\ dx^1 = \cos\theta d\rho-\rho\sin\theta d\theta, \ \ dx^2 = \sin\theta d\rho´\rho\cos\theta d\theta\]de modo que \(dx^1\wedge dx^2 = \rho d\rho\wedge d\theta\). El campo de gauge ahora tiene la forma \(A = A_\rho d\rho+ A_\theta d\theta\). Con este cambio el potencial de Landau es
\[V_\lambda = \f 12\int_0^\infty\int_0^{2\pi}\bp{\f 1{\rho^2}f_{\rho\theta}^2+\overline{D_\rho\phi}D_\rho\phi+\f{1}{\rho^2}\overline{D_\theta\phi}D_\theta\phi+\f{\lambda}4(m^2-\bar\phi\phi)^2}\rho d\rho d\theta \label{eq:4} \tag{4}\]Soluciones vorticiales
Es natural discutir soluciones con simetría rotacional en coordenadas polares. Usaremos las simetrías de rotación y reflexión para reducir el funcional de Landau a sólo la integral sobre la parte radial \(\rho\). Las ecuaciones que se obtengan al variar la energía serán las ecuaciones de movimiento reducidas. Por el principio de criticalidad simétrica, las soluciones a estas ecuaciones reducidas son soluciones de las ecuaciones de campo enteras.
Una realización de la simetría circular que explota la simetría interna de la teoría de Ginzburg-Landau bajo una rotación de fase global \(\tilde R(\al):\phi\ra e^{i\al}\phi\) existe. Considere la acción del grupo de rotaciones \(SO(2)\) bajo la acción combinada de rotaciones y rotaciones de fase \((R(\beta),\tilde R(k\beta))\), donde \(k\) es una constante. Esto es lo que se conoce como un lift o levantamiento (un breve repaso se puede encontrar en mi trabajo sobre homotopía y solitones topológicos) de la acción usual de \(SO(2)\).
La invarianza del campo \(\phi\) ante esta acción requiere que
\[\phi(\rho,\theta+\beta) = e^{ik\beta}\phi(\rho,\theta) \label{eq:5} \tag{5}\]Ecuación \(\eqref{eq:5}\) se satisface si y sólo si
\[\phi(\rho,\theta) = e^{ik\theta}\phi(\rho,0) \label{eq:6} \tag{6}\]Sabemos de la teoría global que el comportamiento en el infinito del campo debe ser de la forma \(\phi_\infty=me^{iN\theta}\), entonces, es claro que tomando el límite de \(\eqref{eq:6}\), \(N=k\). Vamos a asumir, \(N\neq 0\) pues el caso \(N=0\) corresponde a la acción usual de \(SO(2)\).
Infinitesimalmente, el generador de la acción combinada de \(SO(2)\) es \(\bp{\f{\pr}{\pr\theta},iN}\), y el campo es invariante si
\[\f{\pr\phi}{\pr\theta} = iN\phi \label{eq:7} \tag{7}\]Vemos que no tiene acción sobre las componenetes del campo de gauge.
Ahora, queremos imponer la invarianza rotacional de los campos. Para esto, queremos que los campos no dependan de \(\theta\), entonces pediremos que
\[\f{\pr\phi}{\pr\theta} = \f{\pr A_\rho}{\pr\theta} = \f{\pr A_\theta}{\pr\theta} \label{eq:8} \tag{8}\]Entonces, la energía de Landau se transforma en el funcional reducido del que hablamos al inicio de esta sección
\[V_\lambda = \pi\int_0^\infty\bp{\f{1}{\rho^2}\bp{\f{dA_\theta}{d\rho}}^2+\bp{\f{d\phi}{d\rho}}^2+\f{1}{\rho^2}A_\theta^2\phi^2+\f{\lambda}4(m^2-\phi^2)^2}\rho d\rho \label{eq:9} \tag{9}\]Pero esta forma del funcional es debido a la acción usual de \(SO(2)\), entonces para tener una expresión del funcional pero con la acción combinada de \(SO(2)\) debemos insertar \(\eqref{eq:7}\) en \(\eqref{eq:9}\), obteniéndose
\[V_\lambda = \pi\int_0^\infty\bp{\f{1}{\rho^2}\bp{\f{dA_\theta}{d\rho}}^2+\bp{\f{d\phi}{d\rho}}^2+\f{(N-A_\theta)^2}{\rho^2}\phi^2+\f{\lambda}4(m^2-\phi^2)^2}\rho d\rho \label{eq:10} \tag{10}\]Las ecuaciones de movimiento reducidas se hallan fácilmente variando la energía
\[\begin{align*} \f{d^2\phi}{d\rho^2}+\f 1{\rho}\f{d\phi}{d\rho}-\f{1}{\rho^2}(N-A_\theta)^2\phi+\f{\lambda}2(m^2-\phi^2)\phi &=0\\ \f{d^2A_\theta}{d\rho^2}-\f 1{\rho}\f{dA_\theta}{d\rho}+(N-A_\theta)\phi^2 &= 0 \end{align*}\]De acuerdo a la literatura, Harden y Arp calcularon numéricamente la solución para \(N=1\). Plohr y Berger y Chen mostraron rigurosamente que soluciones que satisfacen las condicones de contorno en el infinito existen para todo \(N\neq 0\) y todo \(\lambda>0\). Soluciones se obtuvieron numéricamente usando Python para los casos \(N=1\) y \(\lambda=0.5,1,2\). En la segunda imagen se muestran las energía de las solcuiones para \(N=1,2,3,4,5,6\) y para los casos \(\lambda=0.5,1,2\).
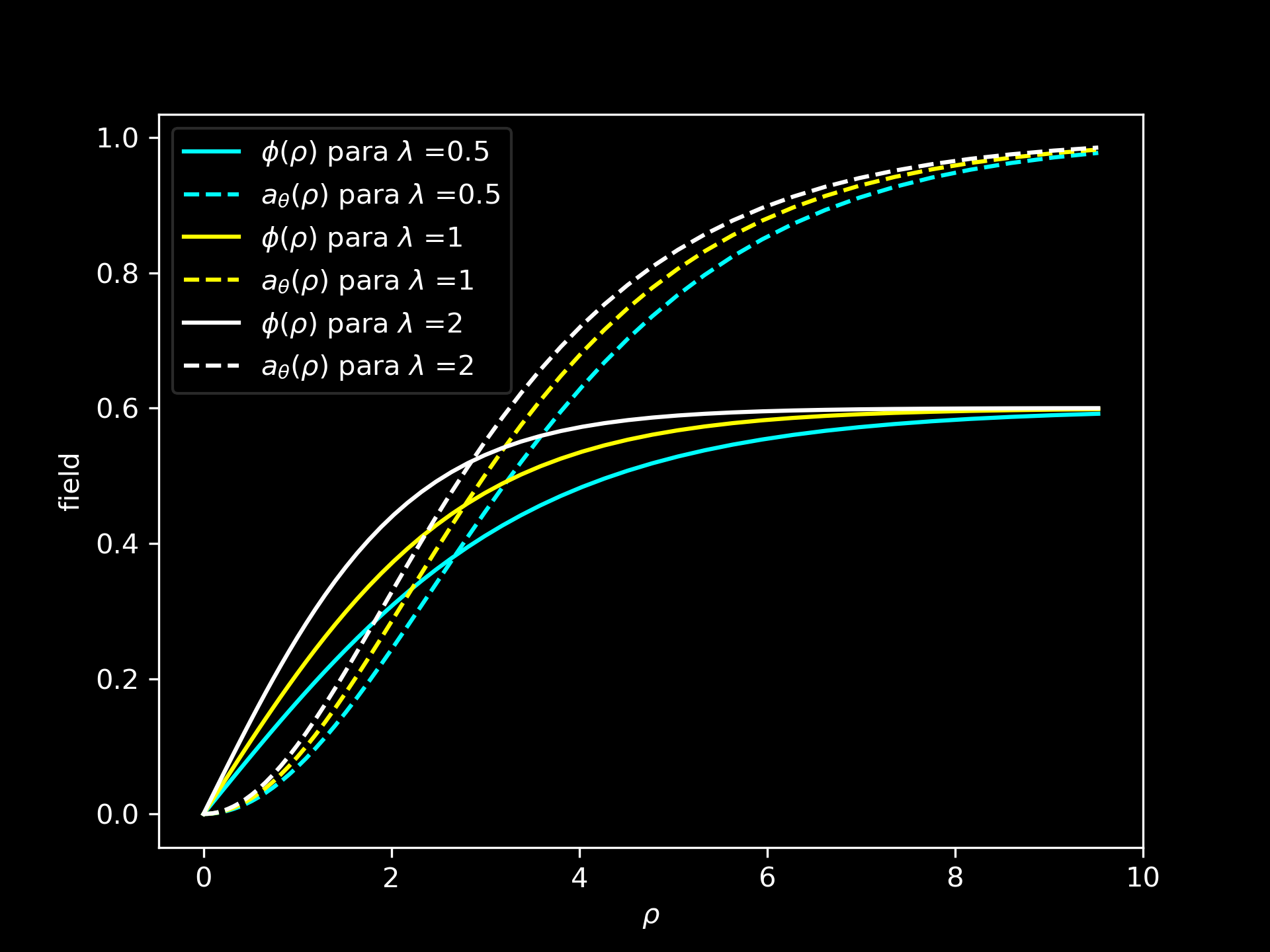
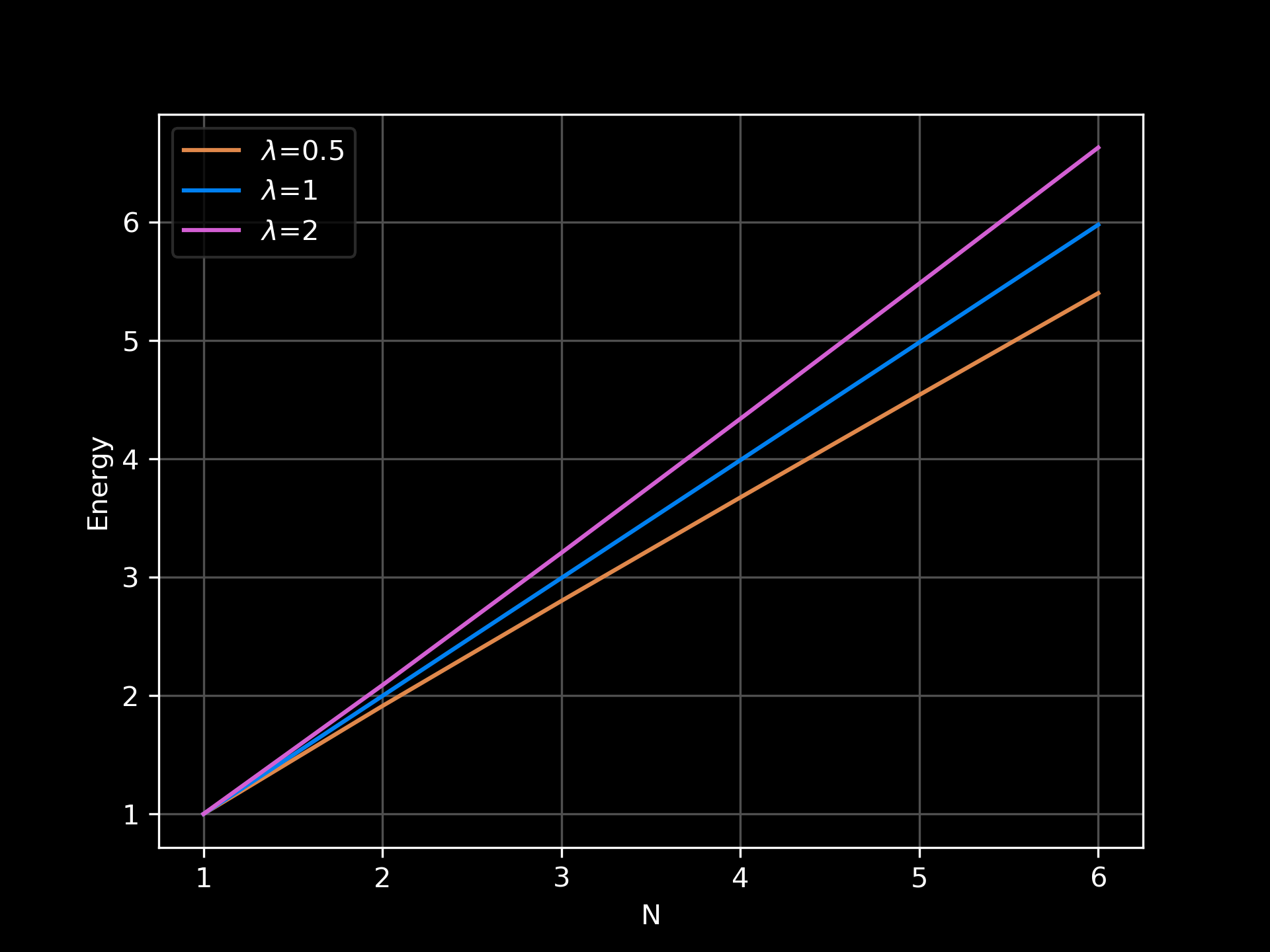
Esto es todo concerniente a las soluciones de la teoría de Ginzburg-Landau gauge. En el siguiente post hablaremos sobre un caso muy particular, \(\lambda=1\), que se conoce como límite de Bogomolny. También analizaremos el Teorema de Taubes que tiene mucho de relación con el límite anterior.