Solitons: Sine-Gordon kink
[physics math Published March 16, 2021
\[\DeclareMathOperator{\Tr}{Tr} \newcommand{\imp}{\implies} % Simbolo de implicacion \newcommand{\supr}[1]{\underset{#1}{\sup}} \newcommand{\mbf}[1]{\mathbf{#1}} % Negrita en modo matemático \newcommand{\lra}{\leftrightarrow} % Flecha derecha e izquierda \newcommand{\h}{\hat} % hat para operadores \newcommand{\red}[1]{\color{red}{#1}} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\blue}[1]{\color{blue}{#1}} \newcommand{\pr}{\partial} % Abreviacion para \partial \newcommand{\cd}{\cdot} % \cdot \newcommand{\cds}{\cdots} % \cdots \newcommand{\inceq}{\subseteq} % incluido e igual \newcommand{\vc}[1]{\vec{#1}} % vector \newcommand{\dg}{^\dagger} \newcommand{\conj}[1]{#1^*} % conjugado \newcommand{\pescalar}[2]{#1\cd #2} % Producto escalar \newcommand{\f}[2]{\frac{#1}{#2}} % Short version for \frac \newcommand{\dott}[1]{\overset{\cdot\cdot}{#1}} % Doble Punto encima (dt) \newcommand{\nab}{\nabla} % Shortcut for nabla %\newcommand{\eval}{\big\rvert} % Raya vertical para indicar evaluación %\newcommand{\deg}[1]{#1^{\circ}} % Grados \newcommand{\la}{\leftarrow} % Leftarrow \newcommand{\mc}[1]{\mathcal{#1}} % Tipografia caligrafia \newcommand{\mf}[1]{\mathfrak{#1}} % Tipografia frakture (gótico) \newcommand{\tf}{\therefore } % Los tres puntitos en triangulo \newcommand{\sder}[2]{\frac{d #1}{d #2}} % Derivada simple de #1 respecto a #2 \newcommand{\der}[3]{\frac{d^{#1}#2}{d #3^{#1}}} % Derivada n-sima de #1 respecto a #2 \newcommand{\sparc}[2]{\frac{\partial #1}{\partial #2}} %Derivadas parciales \newcommand{\parc}[3]{\frac{\partial^{#1}#2}{\partial #3^{#1}}} %Derivada parcial n-esima respecto de #3 \newcommand{\m}[1]{\mathbb{#1}} % Hace una letra R --> \mathbb{R} \newcommand{\inc}{\subset} % Incluido \newcommand{\ndvec}[2]{(#1_1,#1_2,\ldots,#1_{#2})} %Crea un vector #2-dimensional con nombre #1 \newcommand{\ci}{\imath} % Unidad imaginaria \newcommand{\ptodo}{\forall} % Para todo simbolo \newcommand{\me}[1]{#1\m Z} % Multiplos enteros de #1: #1Z. \newcommand{\tq}{\mid} % Simbolo para tal que... \newcommand{\pp}[1]{#1^{\prime\prime}\mkern-1.2mu} %#1´´ \newcommand{\e}[1]{e^{#1}} % Exponencial de #1 \newcommand{\om}{\omega} % Shortcut para omega \newcommand{\Om}{\Omega} % Shortcut para Omega \newcommand{\lam}{\lambda} % Lambda \newcommand{\Lam}{\Lambda} % Lambda mayuscula \newcommand{\al}{\alpha} % alpha \newcommand{\be}{\beta} % beta \newcommand{\gm}{\gamma} % gamma \newcommand{\Gm}{\Gamma} % Gamma \newcommand{\del}{\delta} % Delta \newcommand{\sg}{\sigma} % Sigma \newcommand{\Del}{\Delta} \newcommand{\rel}{\sim} \newcommand{\uvec}[1]{\bm{\hat{\mathbf{#1}}}} % Vector unitario \newcommand{\vct}[1]{\vec{\mathbf{#1}}} \newcommand{\ra}{\rightarrow} \newcommand{\eps}{\epsilon} \newcommand{\ex}{\exists} \newcommand{\bp}[1]{\left(#1\right)} \newcommand{\bb}[1]{\left[#1\right]} \newcommand{\bl}[1]{\left\{#1\right\}} \newcommand{\deld}[1]{\delta^{(3)}(#1)} % Delta de Dirac en 3d \newcommand{\ddrc}[2]{\delta^{(#1)}(#2)} % Delta de Dirac en Nd \newcommand{\lrpr}{\overset{\lra}{\pr}} % left right partial \newcommand{\slashd}{\kern-0.5em\raise0.22ex\hbox{/}} \newcommand{\barra}[1]{\cancel{#1}} \newcommand{\lan}{\langle} \newcommand{\ran}{\rangle}\]
El modelo \(\phi^4\) que vimos en el post anterior no es muy rico en propiedades cuando comenzamos a hablar de soluciones multisolitónicas. En este post trataremos el modelo de Sine-Gordon, en la cual los vacíos están numerados por un entero arbitrario, de modo que configuraciones de campos con cualquier número de solitones están permitidos.
El modelo
La densidad lagrangiana para este modelo es la siguiente
\[\mc L = \f 12\pr_\mu\phi\pr^\mu\phi-(1-\cos\phi). \label{eq:1} \tag{1}\]La ecuación de campo de Sine-Gordon es
\[\pr_\mu\pr^\mu\phi+\sin\phi=0 \label{eq:2} \tag{2}\]Los vacíos de esta teoría se pueden hallar minimizando el potencial. Estos se hallan cuando \(\sin\phi_0=0\), lo que implica que
\[\phi_0 = 2\pi n, \ \ n\in\m Z. \label{eq:3} \tag{3}\]El grupo de homotopía pertinente que clasifica a los solitones de esta teoría es \(\pi_0(\mc V)=\m Z\). Sea \((\phi_.,\phi_+)\) los valores de vacío en el infinito espacial \(x=\pm\infty\) respectivamente. Los solitones topológicos de la teoría están indexados por un entero \(N=(\phi_+-\phi_-)/2\pi\).
El límite de Bogomolnyi para la energía este caso es
\[E\geq\int_{0}^{2\pi N} 2\vert\sin\f\phi 2\vert d\phi = 4\vert N\vert\bb{-\cos\f\phi 2}_0^{2\pi} = 8\vert N\vert \label{eq:4} \tag{4}\]Esta desigualdad se satura cuando el campo satisface alguna de las ecuaciones de Bogomolnyi
\[\phi' = \pm 2\sin\f\phi 2 \label{eq:5} \tag{5}\]Si nos restrigimos a elegir el signo positivo, podemos integrar directamente y obtener
\[\phi(x) = 4\tan^{-1} e^{x-a}, \label{eq:6} \tag{6}\]donde \(a\) es una constante de integración. Ahora nos preguntamos que carga topológica tiene esta solución. Para esto la evaluamos en \(x=\pm\infty\).
\[N = \bp{\f{\phi(+\infty)-\phi(-\infty)}{2\pi}} = 1 \label{eq:7} \tag{7}\]Por lo que esta solución representa un sólo kink. Una representación de la solución \(\eqref{eq:7}\) se muestra en la siguiente figura (donde elegimos \(a=0\)).
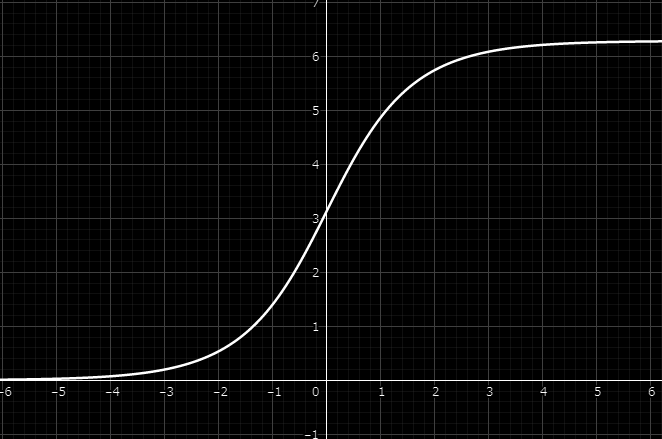
La energía de esta solución es
\[\mc E = 4sech^2(x-a) \label{eq:8} \tag{8}\]Una ilustración de la energía se muestra en la siguiente figura
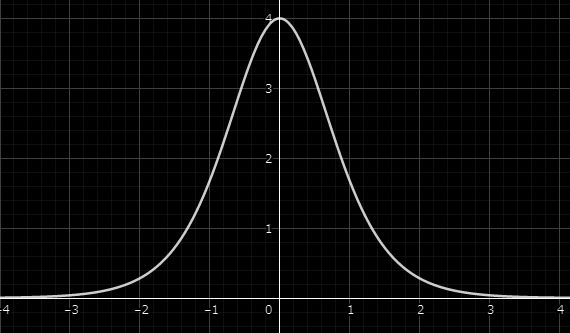
También uno puede comprobar fácilmente que la energía de esta solución es exactamente \(E=8\). Es decir, esta solución satura la desigualdad de Bogomolnyi \(\eqref{eq:4}\).
En el trabajo final que hice para aprobar el curso de Métodos Matemáticos en Física, llamado Teoría de Homotopía y Clasificación de Solitones Topológicos vimos que en \(d\) dimensiones existen dos tipos de solitones topológicos - aquellos en la cual la topología surge de la topología no trivial de la variedad de vacío de un campo lineal en el infinito, cuya carga topológica es un elemento de \(\pi_{d-1}(\mc V)\). El otro tipo es el que contiene un campo no lineal que es constante en el infinito y la carga topológica está asociada con el mapeo entre todo el espacio y una variedad \(Y\), lo que devuelve un elemento del grupo de homotopía \(\pi_d(Y)\). La solución kink del modelo \(\phi^4\) y la del modelo Sine-Gordon pertenecen al primer tipo, sin embargo, el kink del modelo de Sine-Gordon puede pensarse como un soliton del segundo tipo, como veremos a continuación. De hecho también en ese trabajo dijimos que el modelo de Sine-Gordon podía formularse como un campo no lineal pero no lo desarrollamos.
Para formular el modelo de Sine-Gordon como un modelo de campo no lineal, introducimos el vector unitario de dos componentes siguiente
\[\vct \phi = (\phi_1,\phi_2) = (\sin\phi,\cos\phi) \label{eq:9} \tag{9}\]En términos de este vector la densidad lagrangiana \(\eqref{eq:1}\) se escribe como
\[\mc L = \f 12\pr_\mu\vct\phi\cd\pr^\mu\vct\phi-(1-\phi_2)+\nu(1-\vct\phi\cd\vct\phi) ,\label{eq:10} \tag{10}\]donde introdujimos el multiplicador de Lagrange \(\nu\) para asegurar que \(\vct\phi\) esté en la circunferencia \(\vct\phi\vct\phi=1\). El vacío se encuentra en \(\vct\phi=(0,1)\) (ref. \(\eqref{eq:3}\)) en el infinito espacial.
Como el campo \(\vct\phi\) toma el mismo valor en los infinitos \(x=\pm\infty\), podemos identificar los puntos \(x=+\infty\) y \(x=-\infty\). Lo que acabamos de hacer fue compactificar \(\m R\) en \(S^1\).
En cualquier instante, el campo es un mapeo \(\vct\phi:S^1\ra S^1\), donde el dominio es el espacio compactificado y la variedad \(Y=S^1\). A este mapeo se le puede asociar un grado, o winding number, \(N\), el cual también determina su clase en \(\pi_1(S^1)=\m Z\). Este número puede ser calculado como
\[N=\f 1{2\pi}\int_{-\infty}^\infty\eps_{ab}\phi_a'\phi_b dx. \label{eq:11} \tag{11}\]Es claro que este winding number es lo mismo que la carga topológica \(\eqref{eq:7}\) definida anteriormente. En esta formulación, el modelo de Sine-Gordon es un análogo de menor dimensión del modelo sigma y del modelo de Skyrme.