In this post we will cover the classic calculation of Bogomolny and obtain the energy bound. This bound is saturated in a very especial way leading to the linear Bogomolnyi equation, of great importance in the study of solitons. These equations hide a remarkable complex structure of solitons. Results on the dynamics of multivortex solutions are gouped in Taubes Theorem.
In this post we will cover the vortex solutions in the gauged Ginzburg-Landau theory.
In this post we talk about an ancient greek wind instrument called aulos and introduce one of the best history pages on the web.
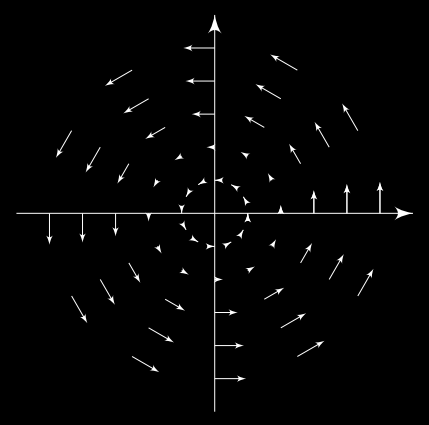
In this post we will cover the vortex solutions in the Ginzburg-Landau theory. We will focus on the global theory only.
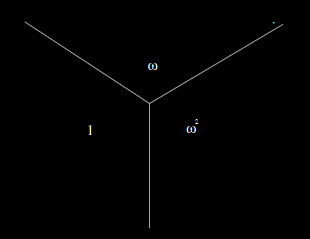
We give a brief discussion about domain wall junctures. This arise as a consecuence of the potencial of having more than two degenerate minima. We also treat the Bogomolny equations for this problem.
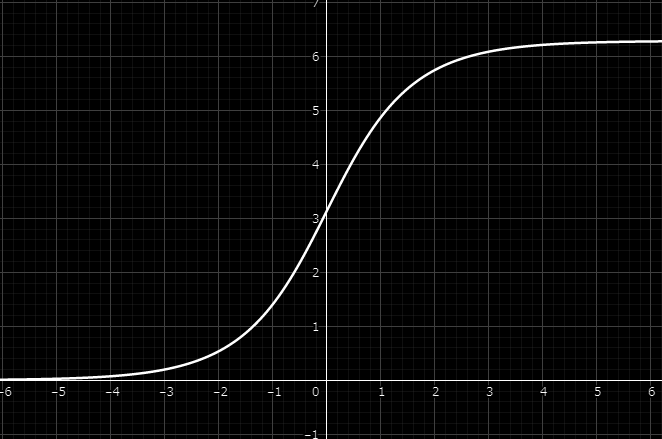
In this post we talk about the Sine-Gordon kink solution. We discuss the Bogomolnyi bound for this case and its non linear realization.
This is part two of the previous post on the greek alphabet and pronunciation.
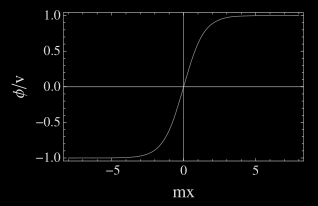
In this post we talk about the most basic soliton, the kink. We review some of its properties and the conserved topological charge.
Finally I pick the courage to start this journey of learning Ancient Greek. In this post we will learn the Greek alphabet and pronunciation.
In this post I present my final assignment for the elective course Seminar on Quantum Mechanics and Information Theory.
In this post I present my work on homotopy theory and its role in the classification of topological solitons in dimensions $d=1,2,3$. This work was the final assignment for approving the course on Mathematical Methods in Mathematical Physics at my university.
This second post will be about the field equations for a gauge theory. This is a direct generalization of Maxwell's equations.
In this post we will treat the Principle of Symmetric Criticality. We will see that this principle is not universally valid. We will also illustrate some examples of application of the principle.
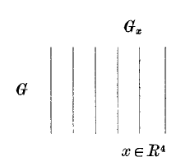
This will be the first in a series of post about concepts in geometry of gauge fields and properties of Yang-Mills equations based on the book of Sir Michael Atiyah, Geometry of Yang-Mills Fields.
Finally, we give introduce the concept of integration of p-forms over p-chains.
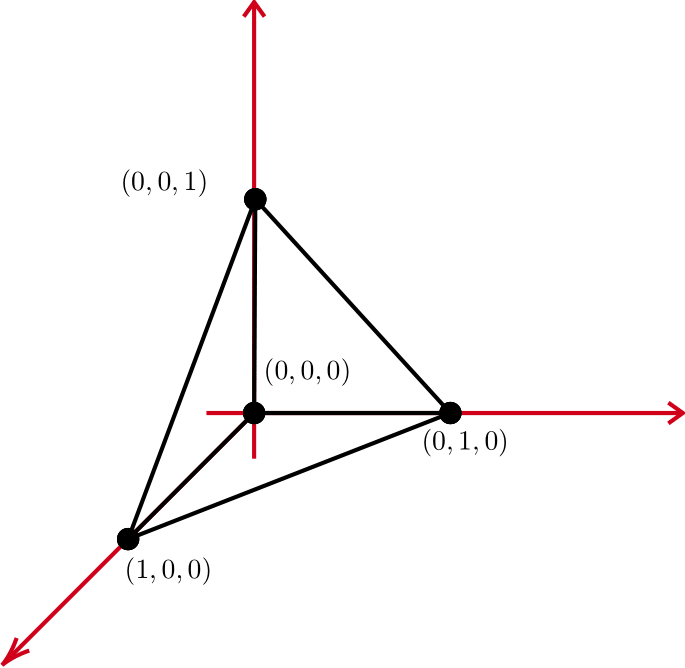
We give an introduction to r-simplexes and r-chains in order to introduce the notion of integration over r-chains.
We review how to find the solution for the electromagnetic four-potential in the Lorentz gauge.
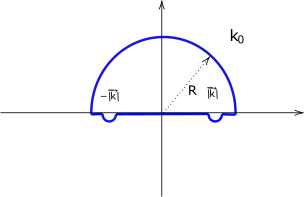
We review how to find the solution for the electromagnetic four-potential in the Lorentz gauge.
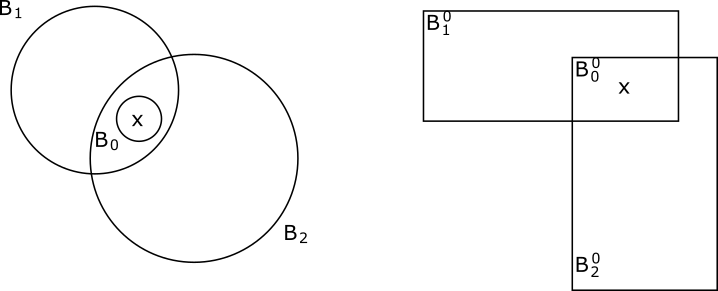
In this second post about topology we introduce the concept of closed subsets and bases for a topology.
This is a short text about the firsts pharaos of Egypt and how the unification happened.
This is the first in a series of post about certain topics of Topology.In this post we treat one of the biulding blocks of Mathematics, that it, Topological Spaces as well as introducing open subsets.
In this blogpost I explain how to create and upload a package to Python Package Index.
In this post I review Spinor representations of SO(2n). Also, we treat Clifford algebra generators and its connection with orthogonal groups.
En este post voy a detallar como instalar Git en Windows .